电子电路与系统基础笔记（2）——电阻与电源

wzf2000
2020年3月22日

电子电路与系统基础笔记（2）——电阻与电源

电路元件——电阻与电源

基本概念

端口与网络

• 端口：terminal
• 端口：port

如果从一个端点流入多少电流，从另一个端点流出同样大小的电流，这两个端点则构成一个端口。

一般端口的电压电流关联参考方向如图所示：

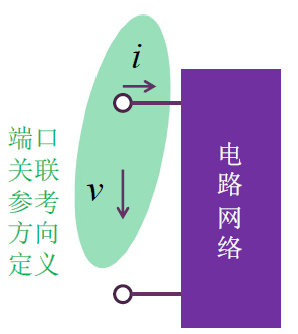
端口条件

准静态条件：$d_{AB} << \lambda \Rightarrow \tau_{AB} = \frac{d_{AB}}{c} << \frac{\lambda}{c} = \frac{1}{f} = T$。才能达到：$i_B \approx i_A$。

不满足准静态条件，则无法定义端口，也就没有电路网络/电路元件的抽象：所有的电路定律都是建立在支路基础上的，此时只能从电磁场角度分析而不能从电路角度分析，分析复杂度急剧增加：电路——有限个端口的电压电流分析，代数方程和微分方程求解；电磁场——连续空间的偏微分方程求解。

单端口网络和多端口网络

封装后对外有 $n$ 个端口，需 $n$ 个方程描述。

广义欧姆定律（别名）：端口描述方程，元件约束条件。

单端口线性电阻：$v(t) = R i(t)$ 即可描述欧姆定律。

端口连接关系 1：串联连接

$$
v = v_1 + v_2 \\
i = i_1 = i_2
$$
串联：电压相加，电流相等。

端口连接关系 2：并联链接

$$
i = i_1 + i_2 \\
v = v_1 = v_2
$$
并联：电流相加，电压相等。

端口连接关系 3：对接连接

$$
v_1 = v_2 \\
i_1 = -i_2
$$
一般视其为并联后总端口开路，也可视为串联后总端口短路。

有源与无源

如果一个网络具有向外部提供电能量的能力，该网络有源（active）；否则无源（passive）。

单端口网络 $p(t) = v(t) i(t)$：

• $p = vi > 0$ 吸收功率，无源。
• $p = vi < 0$ 释放功率，有源。

$n$ 端口网络 $p_\Sigma(t) = \sum\limits_{k = 1}^n v_k(t) i_k(t)$：

• 如果 $p_\Sigma(t) \ge 0(\forall t)$，则无电能向外释放，肯定无源。
• 如果 $p_\Sigma(t)$ 有时大于 $0$，有时小于 $0$，需要讨论。

电阻

可知电阻是无源元件（$p(t) = v(t) i(t) = R \cdot i^t(t) \ge 0$），其消耗电能（转化为热能、光能等）。

电容

而电容功率正负不定（$p_C(t) = C \cdot v(t) \cdot \frac{\mathrm{d} v(t)}{\mathrm{d} t}$），但可根据能量变化表达式：
$$
\Delta E_C(\Delta t) = \frac{1}{2} C v^2(t) - \frac{1}{2} C v^2(t_0)
$$
如果电容初始电压 $v(t_0) = 0$，显然无源。

如果电容初始电压 $v(t_0) \not = 0$，则有源。

电容储能由当前电压决定：如果初始电压不为零，则有源。

考虑到电容初始储能可以全部释放出来，故称电容为无损元件。

无源定义

如果任意满足网络元件约束方程 $f(v, i) = 0$ 的端口电压、端口电流，存在 $t_0$，使得任意 $t \ge t_0$，均有：
$$
\Delta E(t) = \int_{t_0}^t p_\Sigma (t) \mathrm{d} t \ge 0 (\exists t_0, \forall t \ge t_0,\forall v(t), i(t), f(v(t), i(t)) = 0)
$$
则网络则是 $t_0$ 时刻后无源的。

因此电容电感一般被视为无源元件，因为正弦稳态分析时不考虑初值问题。

但又初始电容的电压、有初始电流的电感是有源元件：例如超级电容（大电容）可当电池使用。

线性与非线性

电路网络的电特性（电功能）由端口电压电流关系描述：

• 如果端口电压电流函数关系满足叠加性和均匀性，则为线性电路。
• 如果不满足叠加性或均匀性，则为非线性电路。

（类似线性变换）

非线性电阻：如二极管。

线性电阻、电容、电感

如 $v(t) = f(i(t)) = L \frac{\mathrm{d} i(t)}{\mathrm{d} t}$ 可验证线性。

• 线性电阻：阻值 $R$ 和元件电压、电流无关。
• 线性电容：容值 $C$ 和元件电压、电流无关。
• 线性电感：感知 $L$ 和元件电压、电流无关。

时变与时不变

电路网络的电特性（电功能）由端口电压电流关系描述：

• 端口电压电流关系式中，除了端口电压、端口电流随时间变化外，其他系数参量如果是常量，则为时不变电路。
• 如果其他系数参量随时间变化（且这种变化和端口电压、端口电流无关，是独立的变化），则为时变电路。

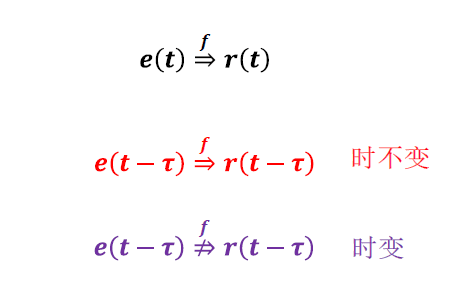
注意时变和非线性没有联系。

理想元件：电阻

电阻

以金属导体为例，假设将电压施加到一段金属导体两端。

在电场作用下，金属的自由电子朝电场反方向运动，运动的电子和金属原子晶格碰撞，阻碍了电子的运动。

• 电阻描述了阻碍电子运动的程度大小。
• 电阻越大，电子运动受到的阻碍越大，电流越小。

$$
R = \rho \frac{l}{S} \\
= \frac{1}{\sigma} \frac{l}{S}
$$

其中 $\rho$ 为电阻率，$\sigma$ 为电导率。

电导

电阻描述的是电子运动受阻碍的程度。

反之，电导描述的则是电子运动的畅通程度。
$$
i = \frac{v}{R} \\
i = G \cdot v \\
G = \frac{1}{R}
$$
电阻伏安特性的斜率为电导导值。

电阻串联

$$
v(t) = v_1(t) + v_2(t) \\
\\
v_1(t) = i_1(t) R_1 = i(t) R_1 \\
v_2(t) = i_2(t) R_2 = i(t) R_2 \\
\\
v(t) = v_1(t) + v_2(t) = i(t) R \\
\\
R = \frac{v(t)}{i(t)} = R_1 + R_2
$$
最后一个式子也就得出了等效电阻的结论。

电阻并联

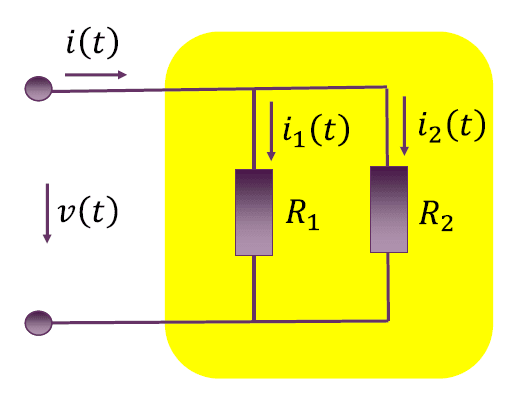
同理可得：
$$
G = G_1 + G_2 \\
R = \frac{1}{G} = \frac{1}{G_1 + G_2} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2}} = \frac{R_1 R_2}{R_1 + R_2}
$$
也就是分析出了等效电导和等效电阻的结论。

前例小结

分析电路就是反复利用基尔霍夫定律（描述端口连接关系）和欧姆定律（描述端口电特性关系），列写电路方程、求解电路方程、对解进行解析的过程。

如果两个电路网络的端口描述方程完全一致，这两个电路网络互为等效电路。

由上例可知，串联、并联线性电阻若封装为单端口网络，则其等效电路均为一个线性电阻，其阻值和导值见上。

电路极端情况

开路：电导值为 $0$：不导电，开路。

短路：电导值为 $\infty$，电阻值为 $0$：电流流动没有任何阻力，短路。

时变电阻：开关

开关是线性还是非线性要看如何连接！

第二个例子是否时变取决于 $v_s$ 是否时变。

理想元件：电源

电源

可产生电动势的器件被称为电源。

• 电源产生的电动势维持电源两端的电位差，驱动外部电路中的电荷源源不断地流动。

根据电源的特性，有两种电源模型：

• 电压源；
• 电流源。

理想电压源

可提供 $v_S(t)$ 的电压，该电压和流经电源的电流大小无关，电压源电流由外接元件决定。

一般被称为恒压源。

注意：电源的电压电流关联参考方向一般和电阻相反。（也就是向外流）

其输出功率：
$$
p = vi > 0
$$
对接关系只需一套端口电压端口电流！（便于图解法分析）

直流电压源，对接关系中，电源释放多少功率，负载就吸收多少功率，能量守恒。（$p_L(t) \equiv p_S(t)$，L——Load，负载；S——Source，电源）

交流电压源称为时变恒压源，也是恒压源。

如正弦波电压源：$v_s(t) = V_{Sp} \cos \omega_0 t$。

其负载吸收功率为：
$$
p_L(t) = \frac{V_{Sp}^2}{2R} + \frac{V_{Sp}^2}{2R} \cos 2 \omega t
$$
也就是瞬时功率。

平均功率为：
$$
\overline{p_L(t)} = \frac{V_{Sp}^2}{2R}
$$

有效值

有效值：effective value：

• rms: root mean square：均方根值；
• 平均功率折合的有效直流幅值。

$$
P_L = \overline{p_L(t)} = \frac{V_{Sp}^2}{2R} + \frac{V_{Srms}^2}{R}
$$

则正弦波电压的有效值显然是：
$$
V_{Srms} = \frac{V_{Sp}}{\sqrt{2}} = 0.707 V_{Sp}
$$
同理可得同时有直流分量和交流分量的电源：
$$
P_L = P_{DC} + P_{AC}
$$
即总功率 $=$ 直流功率 $+$ 交流功率。（对应分量提供的功率）

信号 $=$ 直流分量（平均值）$+$ 交流分量。

理想电流源

可提供 $i_S(t)$ 的电流，该电流和电源两段的电压大小无关，电流源电压由外接元件决定。

同样称为恒流源。

电源串联

• 恒压源和恒压源串联等效于一个恒压源。

• 恒压源和恒流源串联等效于一个恒流源。

• 恒流源和恒流源串联违背 KCL。（电流不相等，实际也肯定不相等）

电源并联

• 恒流源和恒流源并联等效于一个恒流源。
• 恒压源和恒流源并联等效于一个恒压源。
• 恒压源和恒压源并联违背 KVL。（同上）

带内阻电源

实际电源伏安特性曲线偏离理想电压源或理想电流源的伏安特性曲线，这种偏离被建模为内阻。

图示为某太阳能电池的端口伏安特性曲线：

$$
\frac{v}{V_{S0}} + \frac{i}{I_{S0}} = 1
$$

• 将曲线抽象为直线：化曲为直是非线性处理的最基本方法，可以大大简化分析。
• 同时也确实存在具有直线伏安特性的电源。

此切线可以表示为：
$$
v = V_{S0} - i \cdot R_S \\
(R_S = \frac{V_{S0}}{I_{S0}}) \\
i = I_{S0} - v \cdot G_S \\
(G_S = \frac{I_{S0}}{V_{S0}} = \frac{1}{R_S})
$$

流控表述等效电路

有电阻的电压源（$v = v_R + v_S$）。

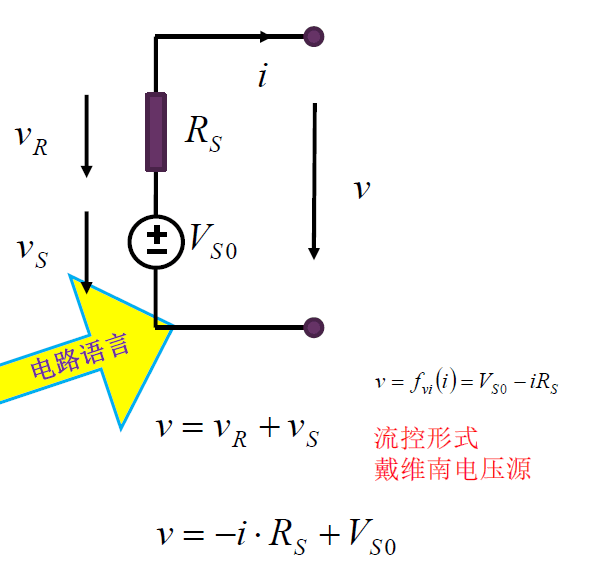
此电压源称为戴维南电压源。

压控表述等效电路

有电阻的电流源（$i = i_G + i_S$）。

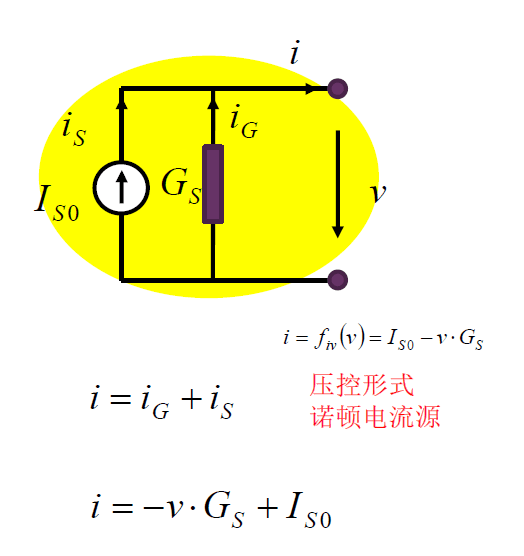
此电流源称为诺顿电流源。

上述两种等效电路分别称为戴维南等效电路和诺顿等效电路。

实例分析

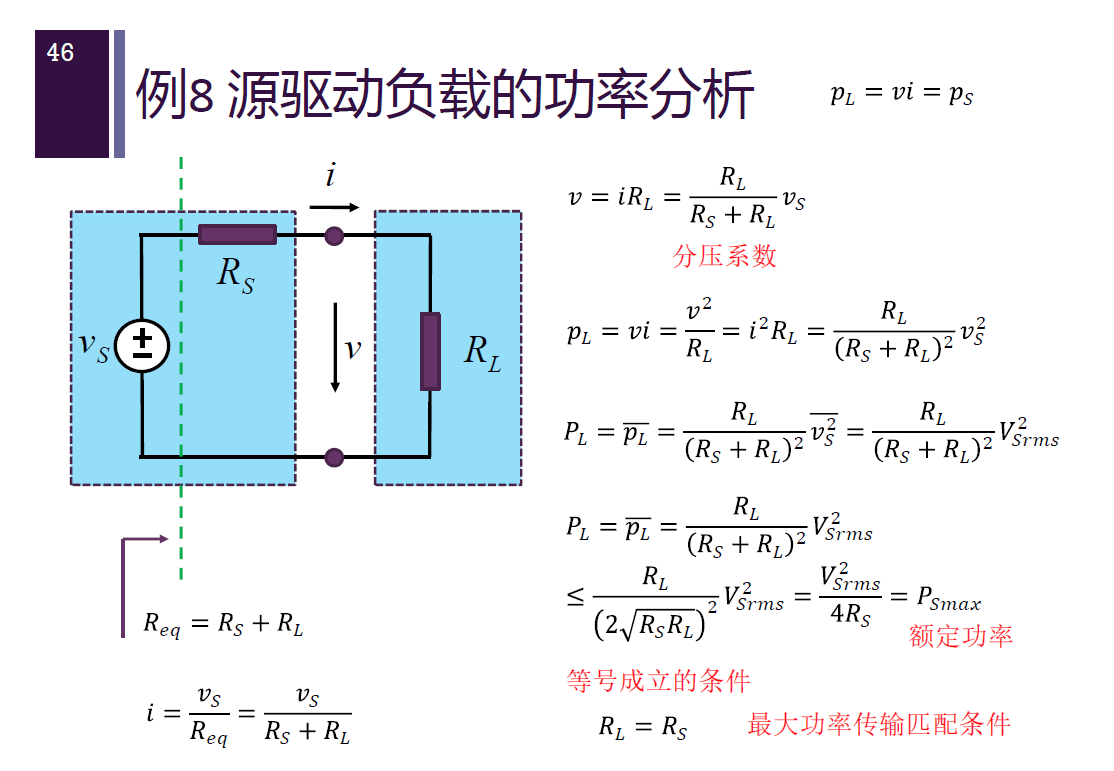
（也可用图解法研究分析，转化为伏安特性曲线上相应面积即可）

直流源和交流源的额定功率

电源的额定功率代表了电源的驱动能力。
源的驱动能力大小由源幅度和内阻共同决定。

对偶原理

电路中的对偶量互换，数学表达式不变。

电路方程中对偶量互换后，形式一样；因而只需研究其一，其二由对偶关系直接获取即可。

小结

• 电磁问题满足准静态条件，则可抽象为电路端口，用电路理论分析电磁问题。

• $n$ 端口网络需要 $n$ 个方程描述其电特性，这 $n$ 个方程被称为 $n$ 端口网络的元件约束方程，或广义欧姆定律方程。

• 能够向端口外提供电能量的网络为有源网络。
• 时变电路和非线性电路的区分：电路参量是否随时间变化？随时间变化是谁导致的？
• 对偶关系。

 电电 笔记