大学物理B笔记22章：光的干涉

sjw1231
2021年12月28日

大学物理B笔记22章：光的干涉

第二十二章 光的干涉

1. 光的相干性

光源：光源发光，是大量原子、分子的微观过程。

普通光源：自发辐射，不同原子、同一原子先后发出的光都是独立的。

激光光源：受激辐射，光完全一样。

光的强度：

对各向同性介质：
$$
E = E_0 \cos (\omega t - kx)
$$
能流密度：
$$
S = |\vec{E} \times \vec{H}| = \varepsilon E_0^2 u \cos^2(\omega t - kx) \quad (\sqrt{\mu} H = \sqrt{\varepsilon} E)
$$
光的强度：
$$
I = \vec{S} = \frac{1}{2} \varepsilon E_0^2 u
$$
在光频波段 $\mu_r \approx 1$：
$$
u = \frac{c}{n}, n = \sqrt{\mu_r \varepsilon_r} = \sqrt{\varepsilon_r}, c = \frac{1}{\sqrt{\mu_0 \varepsilon_0}} \\
u \approx \frac{1}{\sqrt{\varepsilon \mu_0}} \\
I = \overline{S} = \frac{1}{2} \varepsilon E_0^2 u \approx \frac{n}{2 c \mu_0} E_0^2 \propto n E_0^2
$$
光场中一般只考虑电场。

两列光波的叠加：

对于距离 $P$ 分别为 $r_1$ 和 $r_2$ 的两点：
$$
E_1 = E_{10} \cos(\omega t + \varphi_{10}), E_2 = E_{20} \cos(\omega t + \varphi_{20})
$$
则对于 $P$ 点：
$$
E_1 = E_{10} \cos(\omega t - k r_1 + \varphi_{10}), E_2 = E_{20} \cos(\omega t - k r_2 + \varphi_{20}) \\
E = E_1 + E_2 = E_0 \cos (\omega t + \varphi) \\
E_0^2 = E_{10}^2 + E_{20}^2 + 2 E_{10} E_{20} \cos \Delta \varphi \\
\Delta \varphi = \varphi_2 - \varphi_1
$$
同一介质内：
$$
I \propto E_0^2
$$
因此：
$$
I = I_1 + I_2 + 2 \sqrt{I_1 I_2} \cos \Delta \varphi
$$
第三项即为干涉项。

利用复数表示也容易计算。

一般而言：
$$
I = I_1 + I_2 + 2 \sqrt{I_1 I_2} \cdot \overline{\cos \Delta \varphi} \\
\Delta \varphi = (\varphi_{20} - \varphi_{10}) - k (r_2 - r_1)
$$
对于非相干光：
$$
\overline{\cos \Delta \varphi} = 0
$$
对于完全相干光：
$$
\overline{\cos \Delta \varphi} = \cos \Delta \varphi
$$
相光干涉（明）：
$$
\Delta \varphi = \pm 2k \pi, k = 0, 1, 2, \cdots \\
I = I_{\max} = I_1 + I_2 + 2 \sqrt{I_1 I_2}
$$
相消干涉（暗）：
$$
\Delta \varphi = \pm (2k + 1) \pi, k = 0, 1, 2, \cdots \\
I = I_{\min} = I_1 + I_2 - 2 \sqrt{I_1 I_2}
$$
条纹衬比度（对比度，反衬度）：
$$
I = I_1 + I_2 + 2 \sqrt{I_1 I_2} \cdot \cos \Delta \varphi \\
= \frac{1}{2} (I_{\max} + I_{\min}) + \frac{1}{2} (I_{\max} - I_{\min}) \cos \Delta \varphi
$$
定义：
$$
V = \frac{I_{\max} - I_{\min}}{I_{\max} + I_{\min}} \\
= \frac{2\sqrt{I_1 I_2}}{I_1 + I_2}
$$
对于稳定的相位差：频率相同，相位差恒定。

则：
$$
I = (I_1 + I_2) (1 + V \cos \Delta \varphi)
$$
想要观察到稳定的干涉条纹，$V \not = 0$ 且 $\Delta \varphi$ 稳定。

干涉条纹可反映光的全部信息（强度、相位）。

普通光源获得相干光：

分波面法，分振幅法。

2. 双缝干涉及其他分波面干涉实验

双缝干涉：

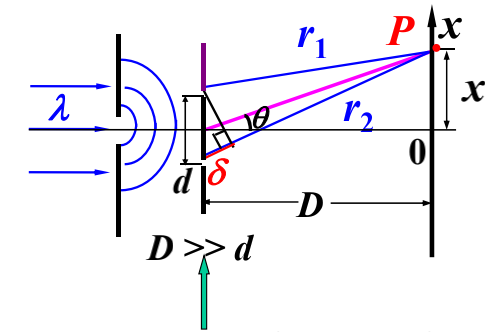
波程差：
$$
\delta = r_2 - r_1 \approx d \sin \theta \approx d \tan \theta = d \frac{x}{D}
$$
相位差：
$$
\Delta \varphi = \frac{\delta}{\lambda} 2 \pi \approx \frac{2 \pi}{\lambda} d \frac{x}{D}
$$
明纹：
$$
\Delta \varphi = \pm 2 k \pi, k = 0, 1, 2, \cdots \\
\delta = \pm k \lambda, x_{\pm k} = \pm k \frac{D}{d} \lambda
$$
暗纹：
$$
\Delta \varphi = \pm (2k + 1) \pi, k = 0, 1, 2, \cdots \\
\delta = \pm (2k + 1) \frac{\lambda}{2}, x_{\pm k} = \pm (2k + 1) \frac{D}{2d} \lambda
$$
条纹间距：
$$
\Delta x = \frac{D}{d} \lambda
$$
双缝干涉光强公式：

设 $I_1 = I_2 = I_0$，则光强为：
$$
I = 4 I_0 \cos^2 \frac{\Delta \varphi}{2}, \Delta \varphi = \frac{d \sin \theta}{\lambda} 2 \pi, k = \frac{d \sin \theta}{\lambda}
$$
双缝干涉条纹的特点：

1. 一系列平行的明暗相间的条纹。

   

2. $\theta$ 不太大时条纹等间距。

3. 中间级次低，两边级次高（即为 $k$）。

4. $\Delta x \propto \lambda$，白光入射时，$0$ 级明纹中心为白色（可用于定 $0$ 级位置），其余级明纹构成彩带，第二级开始出现重叠。

干涉问题分析的要点：

1. 确定发生干涉的光束。
2. 计算波程差（光程差）。
3. 明确条纹特点，包括形状、位置、级次分布、条纹移动等。
4. 求出光强公式、画出光强曲线。

3. 时间相干性

当 $x$ 增大时，干涉现象越来越不明显。

相干长度：

两列波能发生干涉的最大波程差叫相干长度：
$$
\delta_M = k_M \lambda
$$
其中 $\lambda$ 为中心波长。

只有同一波列的分成的两部分，经过不同的路程再相遇时，才能发生干涉。

因此波列长度即为相干长度：
$$
L = \tau c = \delta_M
$$
对于普通单色光，$\delta_M$ 大致为 $10^{-3} \sim 10^{-1}m$。

对于激光，理想情况为 $10^1 \sim 10^2 km$，实际一般为 $10^{-1} \sim 10^1 m$。

相干时间：

光通过相干长度所需时间称为相干时间：
$$
\tau = \frac{\delta_M}{c}
$$
时间相干性的好坏即通过相干长度、相干时间的长短来衡量。

光的非单色性：

实际的光束是波列、准单色光。

准单色光指在某个中心波长（频率）附近有一定波长（频率）范围的光。

对波列 $E(t)$ 作傅里叶变换：
$$
g(\omega) = \sqrt{\frac{2}{\pi}} \frac{E_0 \sin[(\omega - \omega_0) \tau / 2]}{\omega - \omega_0}
$$
波列的能谱为：
$$
I(\omega) = |g(\omega)|^2 = \frac{2 \sin^2[(\omega - \omega_0) \tau / 2]}{\pi (\omega - \omega_0)^2} E_0^2
$$

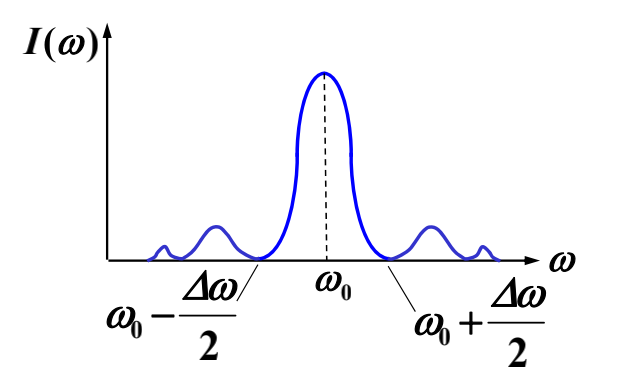
则 $\Delta \omega = \dfrac{2 \pi}{\tau}$，当 $\tau \to \infty$ 时，$\Delta \omega \to 0$。

造成谱线宽度的原因有：

1. 自然宽度。
   $$
   \tau \cdot \Delta E \sim \hbar \\
   \Delta \nu = \frac{\Delta E_i + \Delta E_j}{h}
   $$

2. 多普勒增宽：
   $$
   \Delta \nu \propto \overline{v} \propto \sqrt{T}, T \uparrow \to \Delta \nu \uparrow
   $$

3. 压致增宽（碰撞增宽，统计增宽，$T$ 一定）：
   $$
   \Delta \nu \propto \overline{z} \propto p, p \uparrow \to \Delta \nu \uparrow
   $$

非单色性对干涉条纹的影响：

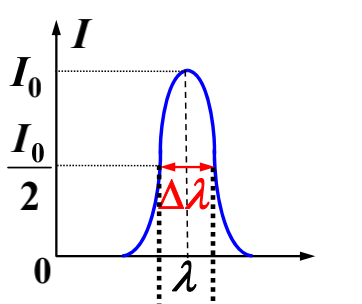
设能产生干涉的最大级次为 $k_M$，则有：
$$
k_M \left(\lambda + \frac{\Delta \lambda}{2} \right) \frac{D}{d} = (k_M + 1) \left(\lambda - \frac{\Delta \lambda}{2} \right) \frac{D}{d}
$$
又因为 $\lambda >> \Delta \lambda$，故：
$$
k_M = \frac{\lambda}{\Delta \lambda}
$$
故：
$$
x_M = k_M \frac{D}{d} \left(\lambda + \frac{\Delta \lambda}{2} \right) \approx k_M \frac{D}{d} \lambda
$$
两列波的最大波程差即为：
$$
\delta_M = k_M \left(\lambda + \frac{\Delta \lambda}{2} \right) \approx k_M \lambda = \frac{\lambda^2}{\Delta \lambda}
$$
即光的单色性越好，相干长度和相干时间就越长，时间相干性就越好。

4. 空间相干性

光源宽度对干涉条纹衬比度的影响。

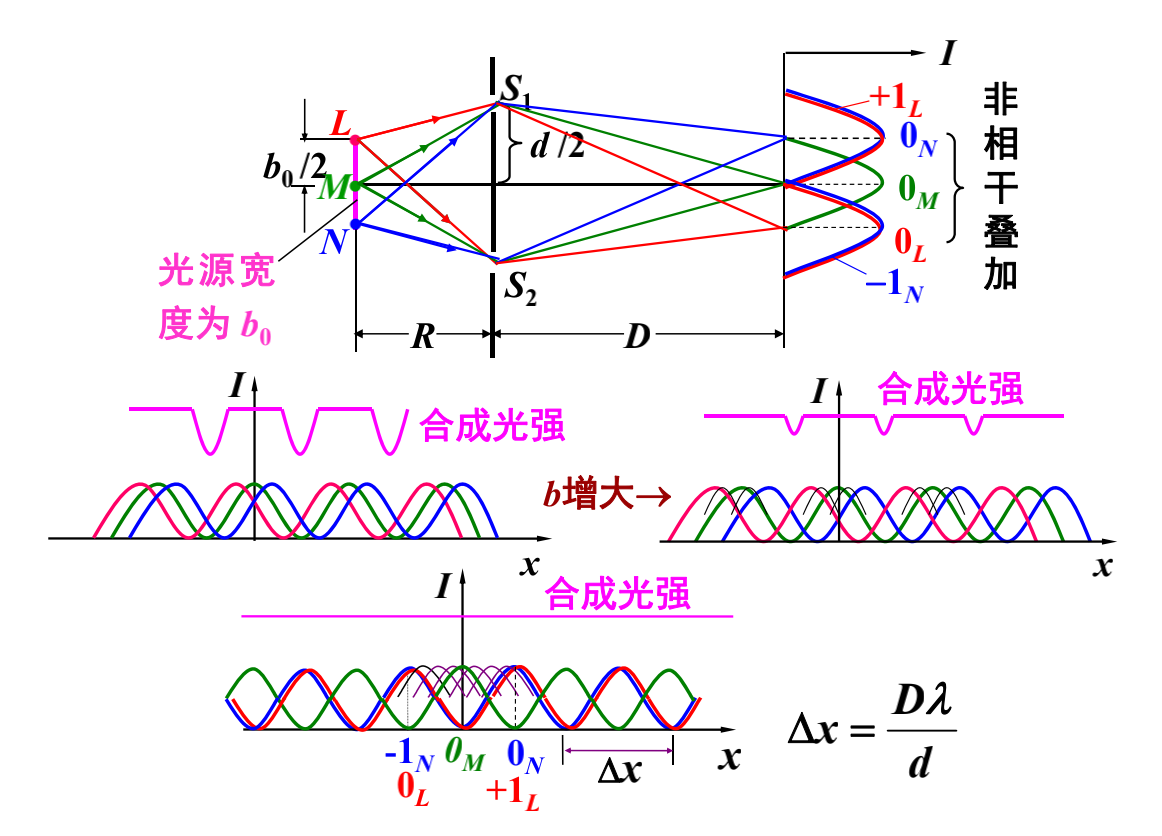
极限宽度：

当光源宽度 $b$ 增大到某个宽度 $b_0$ 时，干涉条纹刚好消失，$b_0$ 称为光源的极限宽度。

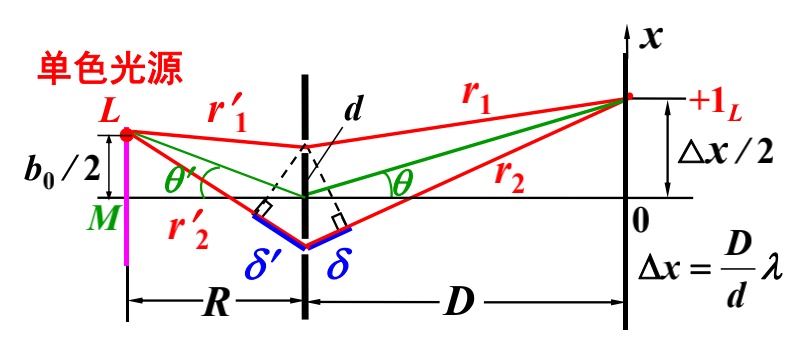
此时 $L$ 端的一级明纹中心在 $x = \dfrac{\Delta x}{2}$ 处。
$$
\left.
\begin{array}{rr}
\text{一级明纹}: & (r_2 + r_2') - (r_1 - r_1') = \delta + \delta' = \lambda \\
D >> d: & \delta \approx d \sin \theta \approx d \dfrac{\Delta x / 2}{D} = \dfrac{\lambda}{2} \\
R >> b_0, R >> d : & \delta' \approx d \sin \theta' \approx d \cdot \dfrac{b_0 / 2}{R}
\end{array}
\right\}
\Rightarrow \frac{d b_0}{2R} = \frac{\lambda}{2} \\
\Rightarrow b_0 = \frac{R}{d} \lambda
$$
当光源宽度 $b < b_0$ 时，才能观察到干涉条纹为观察到较为清晰的干涉条纹，通常取 $b \le b_0 / 4$。相干间隔：

根据：
$$
b < b_0 = \frac{R}{d} \lambda \\ \Rightarrow d < \frac{R}{b} \lambda = d_0 $$ 因此： $$ d_0 = \frac{R}{b} \lambda $$ 称为相干间隔，是光场中正对光源的平面上能够产生干涉的两个次波源间的最大距离。$R$ 一定时，$d_0$ 越大，光场的空间相干性越好。相干孔径角：

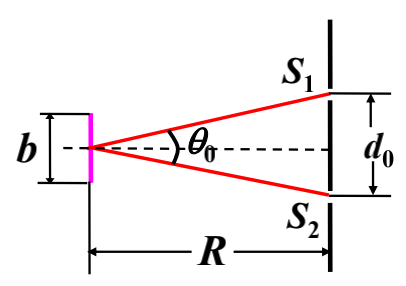
相干间隔也可以用相干孔径角替代：
$$
\theta_0 = \frac{d_0}{R} = \frac{\lambda}{b}
$$
即 $d_0$ 对光源中心的张角。

在 $\theta_0$ 范围内的光场中，正对光源的平面上的任意两点的光振动是相干的。

$\theta_0$ 越大空间相干性越好。

普通单色光源分波面干涉受光源宽度的限制，存在条纹亮度和衬比度的矛盾，而激光光源不受以上限制。

相干间隔应用：

利用空间相干性测要原型体的角直径：
$$
\varphi = \frac{b}{R}
$$
使 $d = d_0$，条纹消失，则：
$$
d_0 = \frac{R}{b} \lambda = \frac{\lambda}{\varphi} \Rightarrow \varphi = \frac{\lambda}{d_0}
$$
考虑衍射影响，则：
$$
\varphi = 1.22 \frac{\lambda}{d_0}
$$
而遥远星体的 $d_0$ 有几到十几米，测量并不方便，所以需要迈克尔孙测星干涉仪，其用四块反射镜增大了双缝的缝间距。

5. 光程

为方便计算光经过不同介质时引起的相差，引入光程的概念。

对于折射率为 $n$ 的介质：
$$
\Delta \varphi = \frac{nr}{\lambda} 2 \pi
$$
这表明，光在介质中传播路程 $r$ 和在真空中传播路程 $nr$ 引起的相位差相同。

我们称 $nr$ 为介质中与路程 $r$ 对应的光程，由此得到关系：
$$
相差 = \frac{光程差}{\lambda} 2 \pi
$$
其中 $\lambda$ 为真空中波长。

透镜不产生附加光程差：

在干涉、衍射装置中经常要用到透镜，光线经过透镜后并不附加光程差。

物点到象点（亮点）各光线之间的光程差为零。

6. 薄膜干涉——等厚条纹

薄膜干涉是分振幅干涉。

日常可见如肥皂泡上的彩色、雨天地上油膜的彩色、昆虫翅膀的彩色。

膜要薄是因为光的相干长度所限。

劈尖干涉：

尖角很小的两个平面所构成的薄膜叫劈尖。
$$
\theta : 10^{-4} \sim 10^{-5} \mathrm{rad} \approx 57 \times (10^{-4} \sim 10^{-5}) \mathrm{degree}
$$
单色平行光垂直入射：

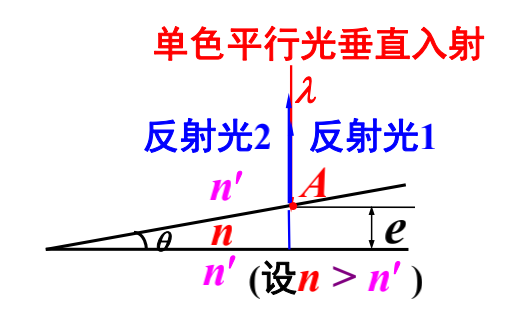
在 $A$ 点，反射光 $1$ 有半波的损失，故光程差为：
$$
\delta(e) \approx 2ne + \frac{\lambda}{2}
$$
因此同一厚度对应同一级条纹——等厚条纹。

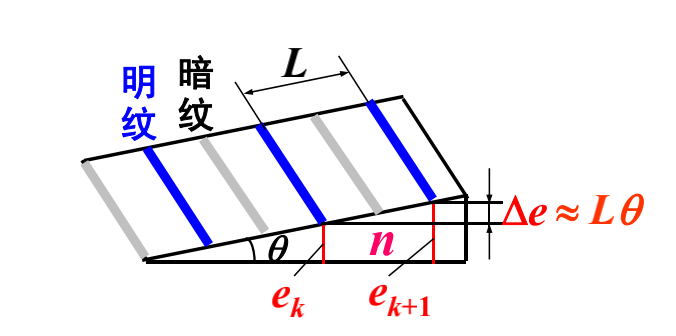
条纹间距：
$$
L \approx \frac{\Delta e}{\theta}
$$
而：
$$
\Delta \delta = 2n \Delta e = \lambda
$$
因此：
$$
L \approx \frac{\lambda}{2n \theta}, \theta \downarrow \to L \uparrow
$$
牛顿环：

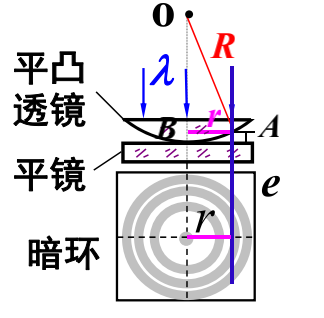
$R$ 很大，大约 $1 \sim 2 m$。

平行光垂直入射，光程差为：
$$
\delta = 2e + \frac{\lambda}{2}
$$
而：
$$
r^2 = R^2 - (R - e)^2 \approx 2 Re \\
\Rightarrow e = \frac{r^2}{2R}
$$
对于暗环，第 $k$ 个暗环半径：
$$
r_k = \sqrt{k R \lambda} \propto \sqrt{k} \\
r_{k + 1} - r_k = \frac{\sqrt{R \lambda}}{\sqrt{k + 1} + \sqrt{k}}
$$
则条纹间距逐渐下降，内圈的条纹级次较低。

对于明环：
$$
r_k = \sqrt{\frac{(2k - 1) R \lambda}{2}}
$$
小结：

• 条纹形状：反映了膜的等厚线。
• 条纹移动：反映了膜厚的变化，可以判断楔角的方位。
• 条纹间距：反映了楔角的大小。（$L \approx \dfrac{\lambda}{2n \theta}$）
• 条纹的疏密（间距）变化：反映了楔角的变化，可判断楔角所在的方位。

劈尖的应用：

根据公式：
$$
L = \frac{\lambda}{2 n \theta}
$$
以及已知量，来测量一个未知量计算剩余的，如测量波长、折射率等。

牛顿环的应用：

根据公式：
$$
r_k = \sqrt{k R \lambda} \propto \sqrt{k} \\
r_{k + m}^2 - r_k^2 = m R \lambda
$$
可用于测量透镜球面的半径 $R$ 和波长 $\lambda$。

7. 薄膜干涉——等倾条纹

点光源照明：

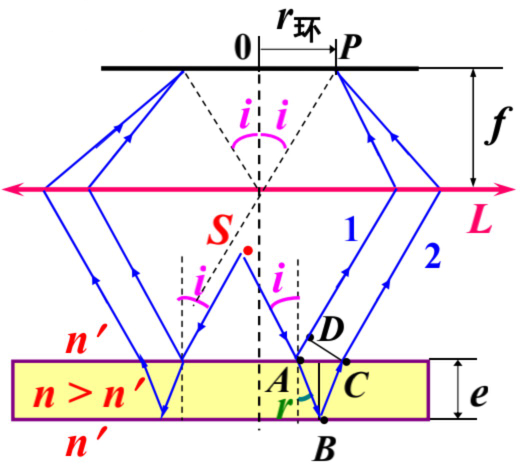
光束 $1, 2$ 的光程差为：
$$
\delta = n(\overline{AB} + \overline{BC}) - n' \overline{AD} + \frac{\lambda}{2} \\
\overline{AB} = \overline{BC} = \frac{e}{\cos r} \\
\overline{AD} = \overline{AC} \cdot \sin i = 2e \tan r \sin i \\
\therefore \delta = \frac{2ne}{\cos r} - \frac{2n' e \sin r \cdot \sin i}{\cos r} + \frac{\lambda}{2}
$$
而又因为：
$$
n' \sin i = n \sin r
$$
因此：
$$
\delta = 2ne \cos r + \frac{\lambda}{2} \\
= 2e \sqrt{n^2 - n'^2 \sin^2 i} + \frac{\lambda}{2} = \delta(i)
$$
明纹：
$$
\delta(i) = k \lambda, k = 1, 2, 3, \cdots
$$
暗纹：
$$
\delta(i) = (2k' + 1) \frac{\lambda}{2}, k' = 0, 1, 2, \cdots
$$
当 $k, k'$ 确定时，$i$ 也一定，即倾角。

$i$ 相同的光线对应同一条干涉条纹——等倾条纹。

条纹特点：

• 形状：一系列同心圆环。

• 条纹间隔分布：内疏外密。
  $$
  \delta = 2ne \cos r + \frac{\lambda}{2} \\
  -2ne \sin r \Delta r = \Delta k \lambda \\
  \Delta r = \frac{\lambda}{2ne \sin r}
  $$

• 条纹级次分布：内高外低，$r_k \downarrow \to i \downarrow \to \delta \uparrow \to k \uparrow$。

• 膜变厚，环纹扩大：$k$ 一定，$e \uparrow \to i \uparrow \to r_k \uparrow$。

• 波长对条纹的影响：$k, e$ 一定，$\lambda \uparrow \to i \downarrow \to r_k \downarrow$。

面光源照明：

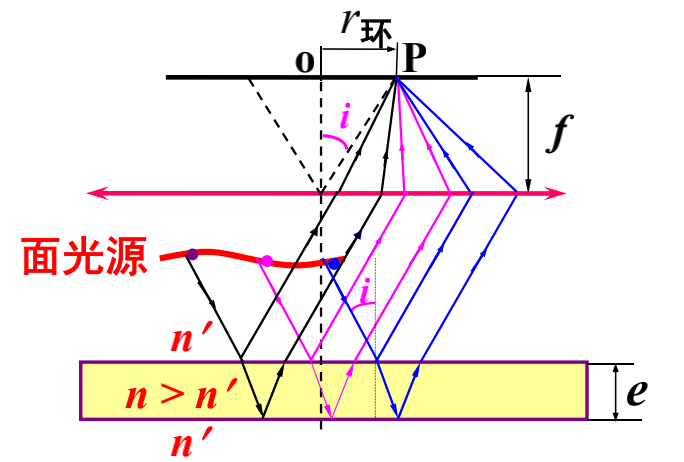
只要 $i$ 相同，都将汇聚于一同一个干涉环上，因而明暗对比更鲜明。

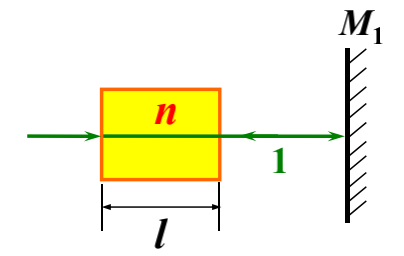
8. 迈克耳孙干涉仪

若 $M_1$ 平移 $\Delta d$ 时，干涉条经过 $N$ 条：
$$
\Delta d = N \cdot \frac{\lambda}{2}
$$
应用：

• 测量微小位移，可精确到 $\dfrac{\lambda}{20}$。

• 测介质折射率，产生附加光程差 $\delta = 2(n - 1)l$，若相应移过 $N$ 个条纹，则有 $\delta = 2(n - 1)l = N\lambda$，由此可得折射率 $n$。

  

 物理 笔记