信号与系统学习笔记（一）

DylanOuO
2021年3月30日

信号与系统学习笔记（一）

特色图像由 $Thorin$ 提供，若造成了惊吓本人概不负责。(造成管理员惊吓，已修改——$MatrixBi$)
绪论部分信号描述分类和简单的运算略。

阶跃信号和冲激信号

函数本身存在不连续点或其导数和积分有不连续点的情况，这类函数统称为奇异信号。

本节主要介绍四类奇异信号，斜变、阶跃、冲激、冲激偶。

单位斜变信号

斜变信号指从某一时刻开始随时间正比例增长的信号。变化率为1则为单位斜变信号。
$$r(t)=\cases{0 &($t<0$)\\ t&($t\geqslant0$)}$$
图像挺显然的就不贴了。

延迟 $-t_0$ ,变斜率加系数

单位阶跃信号

在某点从 $0$ 跳到 $1$ 。
$$u(t)=\cases{0&$(t<0)$\\ 1&$(t>0)$}$$
$t=0$ 处未定义或规定 $u(0)=\displaystyle{\frac{1}{2}}$ 。

图挺显然的就不贴了。

可以用来描述某时刻之前没有信号接入，某时刻接入信号。

若接入信号时间不是 $0$ 而是 $t_0$ ，则用 $u(t-t_0)$ 表示。

某阶跃信号与延时信号之差可以用来表示矩形脉冲，$u(t)-u(t-t_0)$ 即 $0 < t < t_0$ 时为 $1$ ，其他时刻为 $0$.

分段信号可以用各段区间内信号函数乘上该段矩形脉冲表示。

符号函数
$$sgn(t)=\cases{1&$(t>0)$\\ -1&$(t<0)$}\\ =2u(t)-1$$

单位冲激信号

某些信号作用时间短但数值大，需要用特殊的函数来定义。

考虑一个宽度为 $\tau$ ，高为 $\displaystyle{\frac{1}{\tau}}$ 的矩形脉冲，中心为 $t=0$ ，
$$f(t)=\frac{1}{\tau}(u(t+\frac{\tau}{2})-u(t-\frac{\tau}{2}))$$
显然矩形面积为 $1$ ，令 $\tau\rightarrow 0$ ，则函数作用时间趋于零，对时间的积分为 $1$ 。

定义冲激函数（不止可用矩形脉冲定义）
$$\cases{\int_{-\infty}^{\infty}\delta(t)\mathrm{d}t=1\\ \delta(t)=0 \qquad (t\ne0)}$$

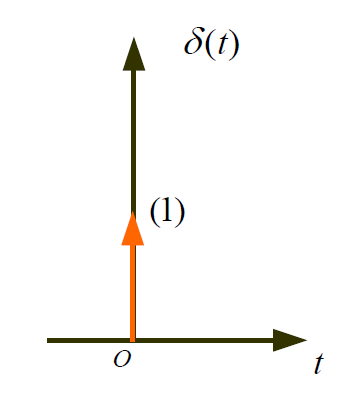
向上箭头表示，周围标上 $1$ 指冲激单位。

用 $\delta(t-t_0)$ 表示 $t_0$ 时刻的冲激。

一些性质。

1. 抽样性（筛选性）

   若 $f(t)$ 在 $t=0$ 处连续且处处有界
   $$\delta(t-t_0)f(t)=f(t_0)\delta(t)\\ \int_{-\infty}^\infty f(t)\delta(t-t_0)\mathrm{d}t=f(t_0)\int_{-\infty}^\infty\delta(t-t_0)\mathrm{d}t=f(t_0)$$

2. 尺度变换
   $$\delta(at+b)=\frac{1}{|a|}\delta(t+\frac{b}{a}),(a\ne0)\\ \int_{-\infty}^\infty\varphi(t)\delta(at+b)\mathrm{d}t=\int_{-\infty}^\infty\varphi(\frac{\tau}{a})\delta(\tau+b)\mathrm{d}(\frac{\tau}{a})\\ =\varphi(-\frac{b}{a})\int_{-\infty}^\infty(-\delta(\tau+b))\mathrm{d}(\frac{\tau}{a})\\ =\varphi(-\frac{b}{a})\int_{-\infty}^\infty\delta(\tau+b)\mathrm{d}(\frac{\tau}{a})\\ =\frac{1}{|a|}\varphi(-\frac{b}{a})\int_{-\infty}^\infty\delta(t)\mathrm{d}t\\ =\int_{-\infty}^\infty\varphi(t)\frac{1}{|a|}\delta(t+\frac{b}{a})\mathrm{d}t$$

3. 冲激函数与阶跃函数的关系
   $$\int_{-\infty}^t\delta(t)\mathrm{d}t=\cases{0&(t<0)\\1&(t>0)}=u(t)\\ \frac{\mathrm{d}}{\mathrm{d}t}u(t)=\delta(t)\\ $$

4. 阶跃函数和单位斜变函数的关系
   $$\frac{\mathrm{d}}{\mathrm{d}t}r(t)=u(t)$$

冲激偶

定义
$$\delta'(t)=\frac{\mathrm d}{\mathrm dt}\delta(t)\\ $$
性质：

1. 取样性
   $$\int_{-\infty}^\infty\delta'(t-t_0)f(t)\mathrm dt=\delta(t-t_0)f(t)|_{-\infty}^\infty-\int_{-\infty}^\infty\delta(t-t_0)f'(t)\mathrm dt\\ =-f'(t_0)\\ \int_{-\infty}^\infty\delta^{(k)}(t-t_0)f'(t)\mathrm dt=(-1)^kf^{(k)}(t_0)$$

2. 冲激偶和冲激函数的关系
   $$\delta'(t)=\frac{\mathrm d}{\mathrm dt}\delta(t)\\ \delta(t)=\int_{-\infty}^t\delta'(t)\mathrm dt$$

3. 奇函数
   $$\delta'(-t)=-\delta'(t)$$

4. 积分
   $$\int_{-\infty}^\infty\delta'(t)\mathrm dt=0$$

5. $$f(t)\delta'(t)=\frac{\mathrm d}{\mathrm dt}(f(t)\delta(t))-f'(t)\delta(t)\\ =f(0)\delta'(t)-f'(0)\delta(t)$$

信号的分解

交流直流

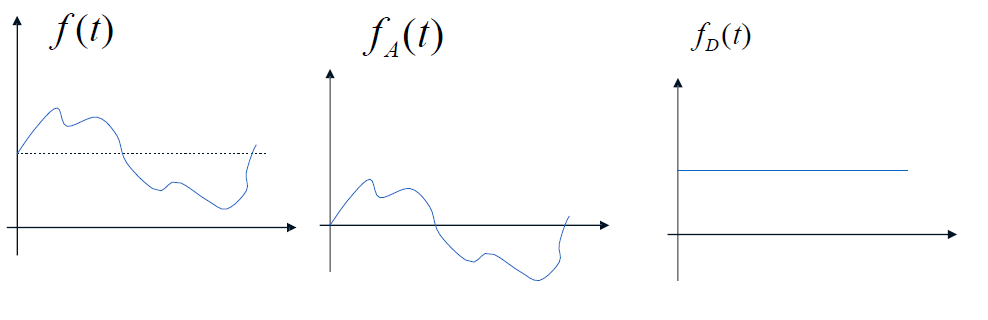
$$f(t)=f_A(t)+f_D(t)\\ f_D(t)=\lim_{T\rightarrow\infty}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)\mathrm dt$$

$$P=\lim_{T\rightarrow\infty}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f^2(t)\mathrm dt\\ =f_D^2(t)+\lim_{T\rightarrow\infty}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_A^2(t)\mathrm dt$$

偶分量和奇分量

$$f_e(t)=\frac{1}{2}[f(t)+f(-t)]\\ f_o(t)=\frac{1}{2}[f(t)-f(-t)]\\ P=\lim_{T\rightarrow\infty}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_o^2(t)\mathrm dt+\lim_{T\rightarrow\infty}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_e^2(t)\mathrm dt$$

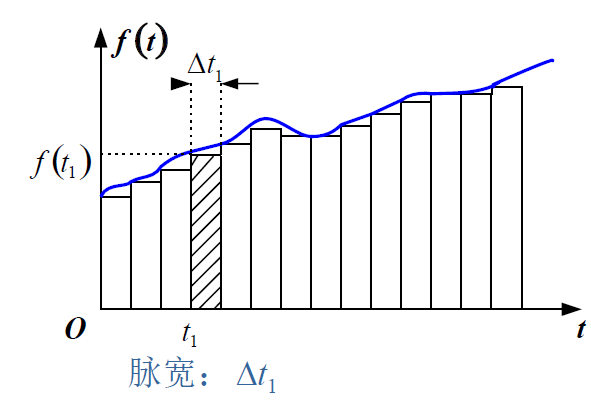
脉冲分量

区间 $t_1 \rightarrow t_1+\Delta t$ 的信号可表示为 $f(t_1)(u(t-t_1)-u(t-t_1-\Delta t))$ ,
$$f(t)=\sum f(t_1)(u(t-t_1)-u(t-t_1-\Delta t))\\ \lim_{\Delta t\rightarrow 0}f(t)=\int_{-\infty}^\infty f(t_1)\frac{\mathrm du(t-t_1)}{\mathrm dt}\mathrm dt_1=\int_{-\infty}^\infty f(t_1)\delta(t-t_1)\mathrm dt_1$$
分解为冲激函数的和

阶跃分量

和上一种比较类似不过横着切
$$f(t)=\int_{-\infty}^\infty\frac{\mathrm df(t_i)}{\mathrm dt_i}u(t-t_i)\mathrm dt_i$$

实部虚部

$$f(t)=f_r(t)+jf_i(t)$$

正交

分解为正交函数集，之后会讲到，为课程主要内容

系统模型

单元框图

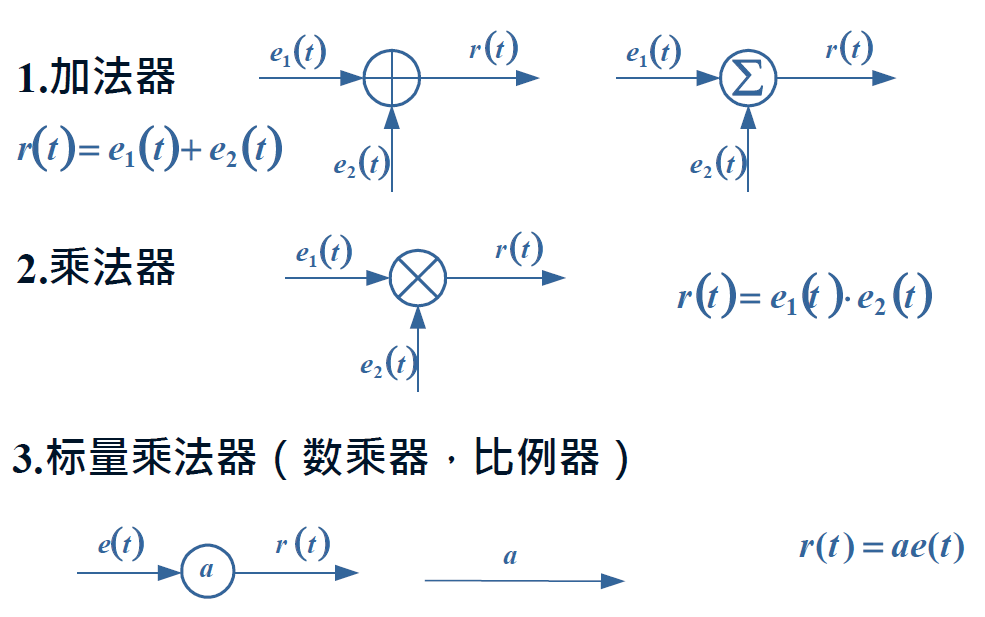
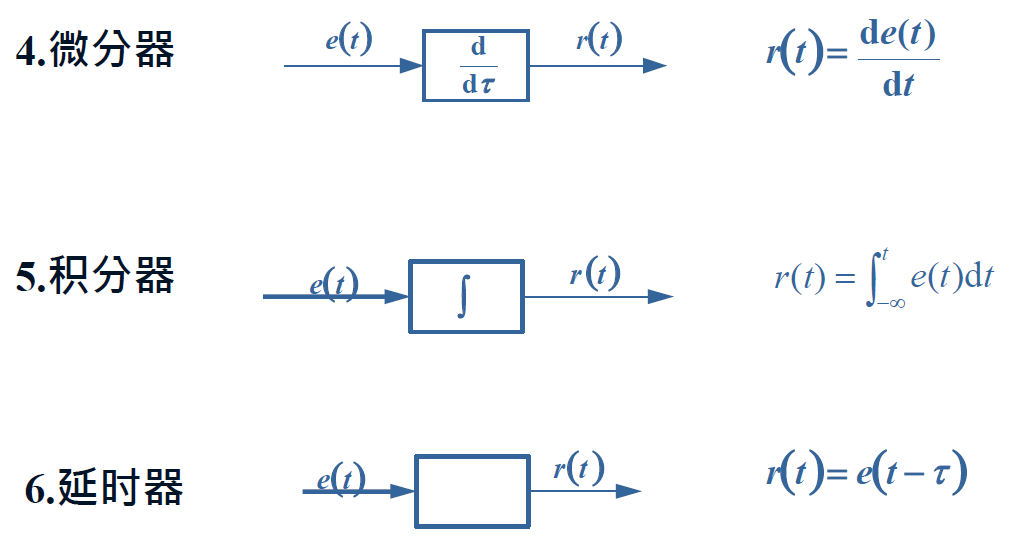
e.g.

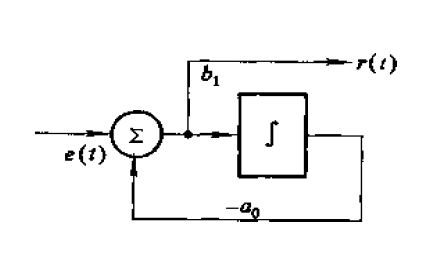
$$e(t)-\frac{a_0}{b_1}\int_{-\infty}^tr(t)\mathrm dt=\frac{r(t)}{b_1}\\ \frac{\mathrm d}{\mathrm dt}r(t)+a_0r(t)=b_1\frac{\mathrm d}{\mathrm dt}e(t)$$

线性时不变因果系统

线性

线性：均匀可叠加

均匀：$e(t)\rightarrow r(t) \Rightarrow ke(t)\rightarrow kr(t)$

叠加：
$$e_1(t)\rightarrow r_1(t),e_2(t)\rightarrow r_2(t)\\ \Rightarrow e_1(t)+e_2(t)\rightarrow r_1(t)+r_2(t)$$

时不变

响应与激励的输入时间无关，即激励延迟后响应延迟相同的时间
$$e(t)\rightarrow r(t)\\ \Rightarrow e(t-t_0)\rightarrow r(t-t_0)$$
可根据方程系数是否随时间改变判断

线性时不变

$$e(t)\rightarrow r(t)\\ \frac{\mathrm d}{\mathrm dt}e(t)\rightarrow \frac{\mathrm d}{\mathrm dt}r(t)\\ \int_{-\infty}^te(t)\mathrm dt\rightarrow \int_{-\infty}^tr(t)\mathrm dt\\ \frac{\mathrm d^{(k)}}{\mathrm dt^{(k)}}e(t)\rightarrow \frac{\mathrm d^{(k)}}{\mathrm dt^{(k)}}r(t)$$

因果

输出不超前于输入

 信号与系统