The Physics of Information Lecture Note 4

The Physics of Information Lecture Note 4

Lecture 4

Introduction to quantum mechanics

Question:

• Is light wave or particle? Wave?
• What determines the light energy? Intensity?

从线性代数到量子力学

photoelectric effects

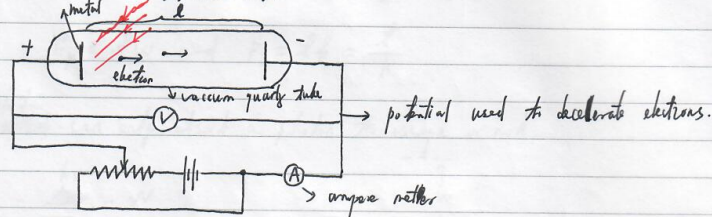
(ampere meter)

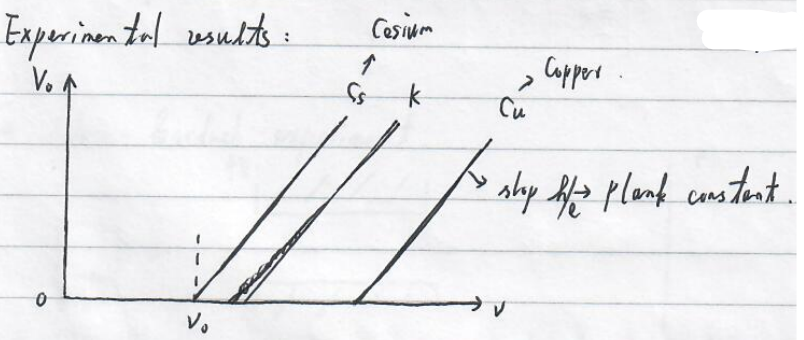
$V_0$ denotes the minimum electric potential(电位，电势) s.t. the electric current vanishes. Thus, $eV_0$ characterizes the kinetic energy of an electron escaped from the metal. It appears that the kinetic energy is independent of the light intensity.

Whether there is current does not depend on the light intensity. $\rightarrow$ The kinetic energy of an escaped electron does not depend on the light intensity.

What is the energy determined by? Light frequency.

It appears that electrons cannot absorb the energy from light continuously. In other words, the light cannot transmit its energy continuously until an electron gains sufficient amount of energy to escape the metal and form a current.

Einstein’s explanation

The light is composed of photons with the energy and momentum determined by

$$E_p=\hbar W\text{ and }p=\frac{\hbar}{\lambda}.$$
An electron can only absorb a photon to escape or not.
$$eV_0=h\nu -W\\ \Rightarrow V_0=\frac{h}{e}\nu -\frac{W}{e}.$$

Stern-Gerlach experiment

$$E=-\vec{\mu}\cdot \vec{B}=-\mu_zB_z$$
where $\vec{\mu}$ is the magnetic moment of an atom.

The force experienced by the atom under an magnetic field is

$$\vec{F}=-\vec{\nabla}E=\mu_z\frac{\partial B_z}{\partial z}\vec{e_z},$$
where we have used $\frac{\partial B_z}{\partial x}=\frac{\partial B_z}{\partial z}=0$.

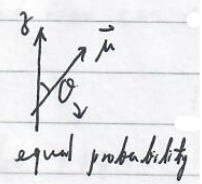
Observed atom density:

• without magnetic fields

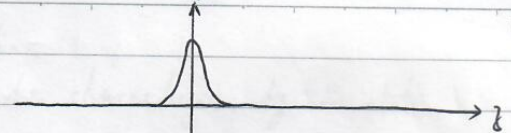
• classical prediction with magnetic fields

• Since electrons of hydrogens do not have orbital angular momentum, quantum prediction with magnetic fields

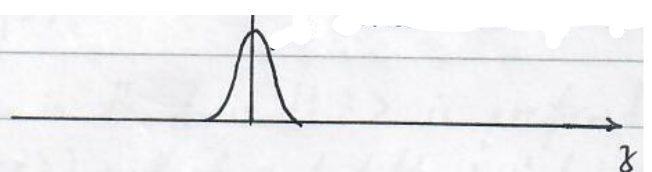
• Experimental observation for hydrogens

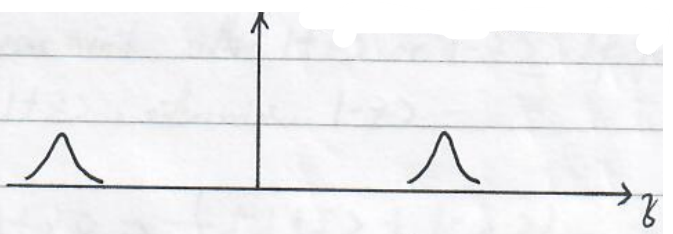
Uhlenbeck and Goudsmit suggested spin of an electron with only two quantified values $\pm \hbar/2$.

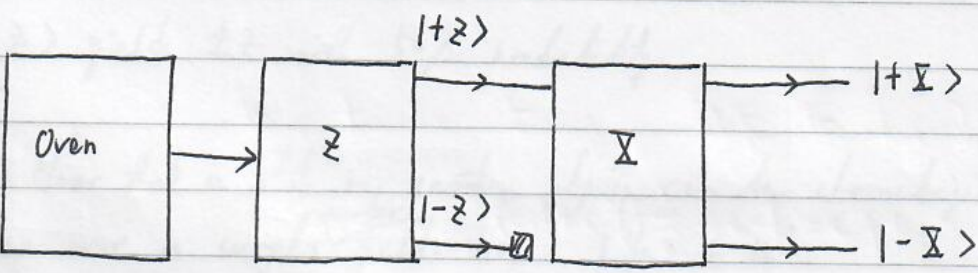
From this observation, we may think that the spin of electrons may be characterized by $\left|\pm Z\right\rangle \left|\pm X\right\rangle$. But this looks strange since there’s no reason that a spin chooses one specific direction. It’s more reasonable if we think the spin as a collection of spin projections with $\hbar /2$ and equal probability since $z$ and $x$ should not be any specific directions. Even if the assumption about the spin electrons are characterized by $\left|\pm Z\right\rangle \left|\pm X\right\rangle$ makes some sense, the following experiment kills this possibility.

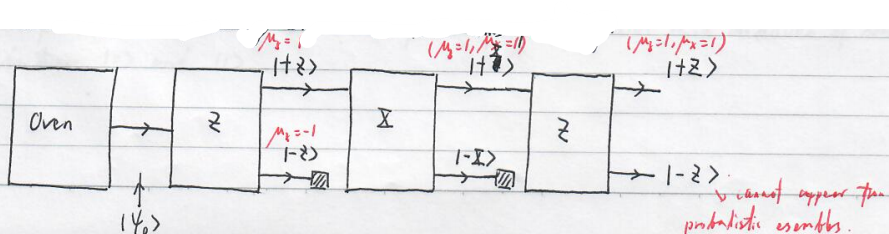
Quantum interpretation

Each atom can be characterized by a state

$$\left|\psi_0\right\rangle =\alpha\left|+Z\right\rangle +\beta\left|-Z\right\rangle ,$$
where $\left|+Z\right\rangle =\binom{1}{0}$ and $\left|-Z\right\rangle =\binom{0}{1}$, $\alpha,\beta \in \mathbb{C}$.

When a measure in the basis $\left|\pm Z\right\rangle$ is performed, we find that atoms exhibit the state $\left|+Z\right\rangle (\left|-Z\right\rangle )$ with the probability $\left|\alpha\right|^2(\left|\beta\right|^2)$. And after the measurement, the state collapses into either $\left|+Z\right\rangle$ or $\left|-Z\right\rangle$. If you observe $+Z$, the state collapses into $\left|+Z\right\rangle$; otherwise, $\left|-Z\right\rangle$.

Since

$$\left|+Z\right\rangle =\frac{1}{\sqrt{2}}(\left|+X\right\rangle +\left|-X\right\rangle )$$
a measurement in the basis $\left|+Z\right\rangle$ gives $\pm X$ with 50% probability. Once we observe $\pm X$, the state collapses into $\left|+X\right\rangle =\frac{1}{\sqrt{2}}(\left|+Z\right\rangle +\left|-Z\right\rangle )$. A further measurement in the basis $\left|+Z\right\rangle$ yields $\pm Z$ with 50% probability.

It’s clear that a state in quantum physics can be characterized by a vector space over a complex number field. Here, $\left|\psi_0\right\rangle \in \mathbb{C}^2$.

Usually, we write

$$\left|+Z\right\rangle =\left|0\right\rangle \text{ and }\left|-Z\right\rangle =\left|1\right\rangle .$$
For a classical bit, it can be either 0 or 1. But here, a quantum bit (qubit) can be a superposition 0 and 1, that is,
$$\left|\psi\right\rangle =\alpha\left|0\right\rangle +\beta\left|1\right\rangle \text{ with }\left|\alpha\right|^2+\left|\beta\right|^2=1.$$
Compared with a classical bit, a qubit can exist in a continuum of states between $\left|0\right\rangle$ and $\left|1\right\rangle$.

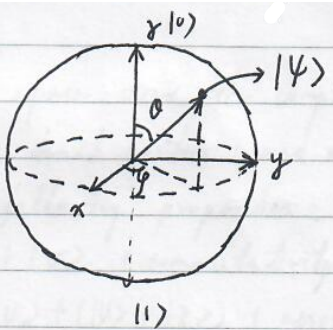
Bloch sphere

Generally, we can write a qubit as

$$\left|\psi\right\rangle =e^{i\gamma} \left(\cos\frac{\theta}{2}\left|0\right\rangle +e^{i\varphi}\sin \frac{\theta}{2}\left|1\right\rangle \right),$$
which can be represented on a Bloch sphere.

To manipulate a single qubit, we can apply appropriate linear operations. For example,

+

$$X\left|0\right\rangle =\left|1\right\rangle \text{ and } X\left|1\right\rangle =\left|0\right\rangle$$

where

$$X=\left( \begin{array}{cc} 0&1\\ 1&0 \end{array} \right).$$

+

$$Y\left|0\right\rangle =i\left|1\right\rangle \text{ and } Y\left|1\right\rangle =-i\left|0\right\rangle$$

where

$$Y=\left( \begin{array}{cc} 0&-i\\ i&0 \end{array} \right).$$

+

$$Z\left|0\right\rangle =\left|0\right\rangle \text{ and } Z\left|1\right\rangle =-\left|1\right\rangle$$

where

$$Z=\left( \begin{array}{cc} 1&0\\ 0&-1 \end{array} \right).$$

• Hadamard gate
  $$H=\frac{1}{\sqrt{2}}\left( \begin{array}{cc} 1&1\\ 1&-1 \end{array} \right).$$

+

$$T=\left( \begin{array}{cc} 1&0\\ 0&e^{i\pi/4} \end{array} \right)=e^{i\pi/8}\left( \begin{array}{cc} e^{-i\pi/8}&0\\ 0&e^{i\pi/8} \end{array} \right)=e^{i\pi/8}\cdot e^{-i\frac{\pi}{8}\sigma_Z}.$$

The Hadamard and $\pi/8$ gate constitute a set of universal gates for unitary single qubit operations.

Review of linear algebra

1. Let $V$ be a vector space over the complex number field $\mathbb{C}$. $\forall \left|v\right\rangle ,\left|u\right\rangle \in V$ (vectors, read as ket), $\left|v\right\rangle +\left|u\right\rangle \in V$ and $\forall \alpha \in \mathbb{C},\alpha\left|v\right\rangle \in V$ with the following properties:
   1. $\left|v\right\rangle +\left|u\right\rangle =\left|u\right\rangle +\left|v\right\rangle$ (commutativity of addition)
   2. $(\left|v\right\rangle +\left|u\right\rangle )+\left|z\right\rangle =\left|v\right\rangle +(\left|u\right\rangle +\left|z\right\rangle )$ (associativity of addition)
   3. There exists a zero element s.t. $\left|v\right\rangle +0=0+\left|v\right\rangle =\left|v\right\rangle$.
   4. There exists an inverse element $\left|y\right\rangle \in V$ s.t. $\left|v\right\rangle +\left|y\right\rangle =\left|y\right\rangle +\left|v\right\rangle =0$.
   5. $1\left|u\right\rangle =\left|u\right\rangle$.
   6. $\forall a,b\in\mathbb{C}, (ab)\left|v\right\rangle =a(b\left|v\right\rangle )$.
   7. $a(\left|u\right\rangle +\left|v\right\rangle )=a\left|u\right\rangle +a\left|v\right\rangle$.
   8. $(a+b)\left|v\right\rangle =a\left|v\right\rangle +b\left|v\right\rangle$.
2. Let $V\equiv \mathbb{C}^n.\forall \left|u\right\rangle \in \mathbb{C}^n,$
   $$\left|u\right\rangle =\left( \begin{array}{c} u_1\\ u_2\\ \vdots\\ u_n \end{array}\right).$$

3. Basis

   Let $V$ be a finite-dimensional vector space. There exists a linearly independent set $\beta=\{\left|v_1\right\rangle ,\left|v_2\right\rangle ,\dots,\left|v_n\right\rangle \}$ s.t. for any vector $\left|v\right\rangle \in V$, it can be uniquely expressed as a linear combination of vectors in $\beta$, i.e.
   

   $$\left|v\right\rangle =\sum_{j=1}^n\alpha_j\left|v_j\right\rangle .$$
   For example, $\{\left|0\right\rangle ,\left|1\right\rangle \}$ and $\{\frac{1}{\sqrt{2}}(\left|0\right\rangle +\left|1\right\rangle ),\frac{1}{\sqrt{2}}(\left|0\right\rangle -\left|1\right\rangle )\}$ are the bases of $\mathbb{C}^2$.
   $$[\left|v\right\rangle ]_{\beta}=\left( \begin{array}{c} \alpha_1\\ \alpha_2\\ \vdots\\ \alpha_n \end{array} \right)$$
   is a coordinate vector of $\left|v\right\rangle$ relative to $\beta$.

4. Inner product

Let $V$ be a vector space, $\forall x,y,z\in V$ and $c\in\mathbb{C}$.	Notation in quantum mechanics
$\left\langle x+z,y\right\rangle =\left\langle x,y\right\rangle +\left\langle z,y\right\rangle$	$(\left\langle x\right|+\left\langle z\right|)\left\langle y\right|=\left\langle x\mid y\right\rangle +\left\langle z\mid y\right\rangle$
$\left\langle cx,y\right\rangle =c\left\langle x,y\right\rangle$	$\left\langle cx\mid y\right\rangle =c^*\left\langle x\mid y\right\rangle$ where $c^*$ is the complex conjugate
$\overline{\left\langle x,y\right\rangle }=\left\langle y,x\right\rangle$ complex conjugate	$(\left\langle x\mid y\right\rangle )^*=\left\langle y\mid x\right\rangle$
$\left\langle x,x\right\rangle >0$ if $x\ne 0$	$\left\langle x,x\right\rangle >0$ if $\left|x\right\rangle \ne 0$
Let $V=\mathbb{C}^n$, $\left\langle x,y\right\rangle =\sum_j x_j\overline{y_j}$	Let $V=\mathbb{C}^n$, $\left\langle x\mid y\right\rangle =\sum_j x_j^*y_j$

A vector space endowed with a specific inner product is called inner product space. In quantum competition and information, we consider a finite-dimensional inner product space, which is the same thing as Hilbert space.

5. Orthonormal basis

   provided that $\left\langle v_i\mid v_j\right\rangle =\delta_{ij}$.

6. Linear operator

   

   

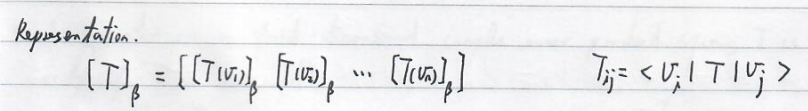
7. Diagonalization and eigenvalues

   

8. Adjoint of a linear operator

   Let $T:V\to V$ be a linear operator. $\forall x,y\in V$,
   

   $$\left\langle x,T(y)\right\rangle =\left\langle T^*(x),y\right\rangle .$$
   $T^*$ is the adjoint of $T$. In quantum physics, for a linear operator $T$, use $T^+$ to denote the adjoint of $T$.

   In quantum physics, for a linear operator $T$, use $T^{\dagger}$ to denote the adjoint of $T$.
   

   $$\left\langle v\mid Tu\right\rangle =\left\langle T^{\dagger}v\mid u\right\rangle =(T^{\dagger}\left|v\right\rangle )^{\dagger}\left|u\right\rangle =\left\langle v\mid T\mid u\right\rangle$$
   

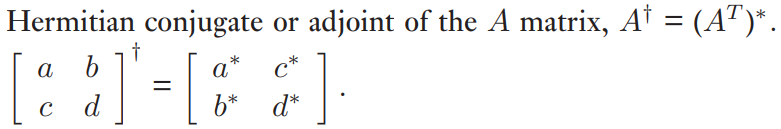
9. Normal and Hermitian operators

Linear algebra	quantum mechanics
$T^*T=TT^*$	$T^\dagger T=TT^\dagger$

An operator on a finite-dimensional complex inner product space, $T$ is diagonalizable iff $T$ is normal.

$T^*=T$	$T^\dagger=T$
Self-adjoint	Hermitian

A normal operator is Hermitian iff it has real eigenvalues.

10. Unitary operator
    

    $T^*T=TT^*=I$	$T^\dagger T=TT^\dagger=I$
    $\left\langle T(x),T(x)\right\rangle =\left\langle x,x\right\rangle$	$\left\langle T(x)\mid T(x)\right\rangle =(T\left|x\right\rangle )^\dagger T\left|x\right\rangle =\left\langle x\mid T^\dagger T\mid x\right\rangle =\left\langle x\mid x\right\rangle$

    Unitary operators are normal and hence diagonalizable.

    Unitary operators are norm-preserving and invertible.
    

    $$\left\langle Au\mid Av\right\rangle =\left\langle u\mid v\right\rangle$$
    All eigenvalues $\lambda_j$ of a unitary operator have modulus 1, that is, $\left|\lambda_j\right|^2=1$.

11. Tensor products

    Let $V$ and $W$ be vector spaces of dimension $m$ and $n$ respectively. Then, $V\otimes W$ ($V$ tensor $W$) is a vector space of dimension $mn$. $V\otimes W$ is composed of linear combinations of $\left|v\right\rangle \otimes \left|w\right\rangle$ (or written as $\left|v\right\rangle \left|w\right\rangle ,\left|v,w\right\rangle$ or $\left|vw\right\rangle$) with $\left|v\right\rangle \in V$ and $\left|w\right\rangle \in W$. The tensor product is defined to have the following rules

    1. $\forall a\in \mathbb{C},$
       $$(a\left|v\right\rangle )\otimes \left|w\right\rangle =\left|v\right\rangle \otimes (a\left|w\right\rangle ).$$

    2. $\forall \left|v_1\right\rangle ,\left|v_2\right\rangle \in V,$

       $$(\left|v_1\right\rangle +\left|v_2\right\rangle )\otimes\left|w\right\rangle =\left|v_1\right\rangle \otimes\left|w\right\rangle +\left|v_2\right\rangle \otimes\left|w\right\rangle .$$

    3. $\forall \left|w_1\right\rangle ,\left|w_2\right\rangle \in W,$

       $$\left|v\right\rangle \otimes(\left|w_1\right\rangle +\left|w_2\right\rangle )=\left|v\right\rangle \otimes\left|w_1\right\rangle +\left|v\right\rangle \otimes\left|w_2\right\rangle .$$

    • Inner product is defined as
      $$(\left|v_1\right\rangle \otimes\left|w_1\right\rangle )(\left|v_2\right\rangle \otimes\left|w_2\right\rangle )=\left\langle v_1\mid v_2\right\rangle \cdot \left\langle w_1\mid w_2\right\rangle .$$

    Provided $\{\left|v_1\right\rangle ,\left|v_2\right\rangle ,\dots,\left|v_m\right\rangle \}$ and $\{\left|w_1\right\rangle ,\left|w_2\right\rangle ,\dots,\left|w_n\right\rangle \}$ are orthonormal bases for $V$ and $W$ respectively, then $\left|v_i\right\rangle \otimes \left|w_j\right\rangle$ with $i=1,\dots,m$ and $j=1,\dots,n$ constitute an orthonormal basis for $V\otimes W$.

• Linear operators of tensor product space

  Let $T:V\to V$ and $S:W\to W$ be linear operators. Define $T\otimes S:V\otimes W\to V\otimes W$ by
  

  $$T\otimes S(\left|v\right\rangle \otimes \left|w\right\rangle )=(T\left|v\right\rangle )\otimes(S\left|w\right\rangle )$$
  for any $\left|v\right\rangle \in V$ and $\left|w\right\rangle \in W$.

  Since $T\otimes S$ is linear,
  

  $$T\otimes S\sum_{ij}a_{ij}\left|v_i\right\rangle \otimes\left|w_j\right\rangle =\sum_{ij}a_{ij}T\otimes S(\left|v_i\right\rangle \otimes\left|w_j\right\rangle )=\sum_{ij}a_{ij}(T\left|v_i\right\rangle )\otimes (S\left|w_j\right\rangle ).$$
  In matrix language,
  $$A\otimes B= \begin{bmatrix} A_{11}B&A_{12}B&\ldots&A_{1n}B\\ \vdots&\vdots&&\vdots\\ A_{n1}B&A_{n2}B&\ldots&A_{nn}B \end{bmatrix}.$$
  Example. Consider 2 qubits. A state of this system is described by
  $$\left|\psi\right\rangle =\sum_{i,j\in\{0,1\}}a_{ij}\left|i\right\rangle \otimes \left|j\right\rangle .$$
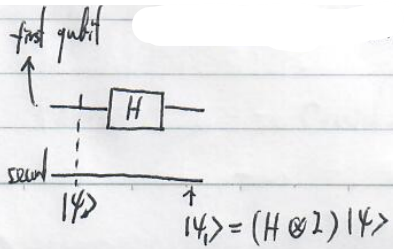
  For example, $\left|\psi\right\rangle =\left|0\right\rangle \otimes\left|0\right\rangle$. We can apply the Hadamard operation only on the first qubit, which is described by
  $$(H\otimes I)\left|\psi\right\rangle =(H\left|0\right\rangle )\otimes \left|0\right\rangle =\frac{1}{\sqrt{2}}(\left|0\right\rangle +\left|1\right\rangle )\otimes \left|0\right\rangle$$
  If $\left|\psi\right\rangle =\frac{1}{\sqrt{2}}(\left|0\right\rangle \otimes \left|0\right\rangle +\left|1\right\rangle \otimes \left|1\right\rangle )$,
  $$\begin{align} \left|\psi_1\right\rangle =(H\otimes I)\left|\psi\right\rangle &=\frac{1}{\sqrt{2}}(H\otimes I\left|0\right\rangle \otimes\left|0\right\rangle +H\otimes I \left|1\right\rangle \otimes\left|1\right\rangle )\\ &=\frac{1}{\sqrt{2}}\left((\left|0\right\rangle +\left|1\right\rangle )\otimes \left|0\right\rangle +(\left|0\right\rangle -\left|1\right\rangle )\otimes\left|1\right\rangle \right). \end{align}$$
  

 The Physics of Information 信息物理