
离散数学笔记(15)——树和平面图
树与生成树
树
数的相关定义
一个连通无回路的无向图 $T$,称之为树。
树叶:度数为 $1$ 的结点,称为树叶。
分支结点:度数大于 $1$ 的结点。
森林:一个无向图的每个连通分支都是树。
相关定理
定理 1:与树定义等价的几个命题:
- $T$ 是无回路的连通图。
- $T$ 无环且每对结点之间有一条且仅有一条道路。
- $T$ 无回路但在任一对不相邻的顶点间添加一条新边 $e$,则 $T + e$ 包含唯一的圈。
- $T$ 是连通的,且每条边都是割边。
- $T$ 是连通的且 $m = n – 1$。
- $T$ 无回路且 $m = n – 1$。
定理 2:每一非平凡树至少有两片树叶。
生成树
定义
如果图 $G$ 的生成子图是树,则称此树为 $G$ 的生成树。
弦:图 $G$ 中,不在其生成树里的边,称作弦。所有弦的集合,称为该生成树的补。
定理:连通图 $G$ 至少有一棵生成树。
赋权图的最小生成树
一棵生成树中的所有边的权之和称为该生成树的权。
具有最小权的生成树,称为最小生成树。
求最小生成树算法——Kruskal 算法(贪婪、贪心)
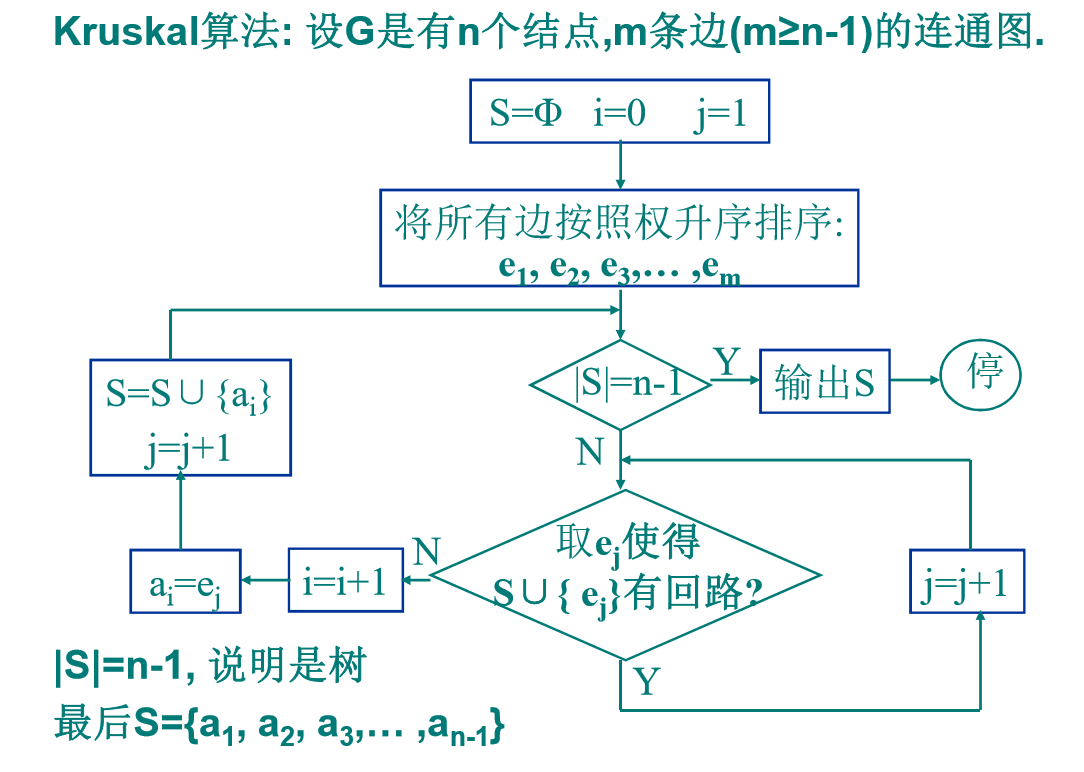
正确性证明:

根树及其应用
有向树
如果 $G$ 是个有向图,且若不考虑边的方向时(即看成无向图时),是一棵树,则称 $G$ 是有向树。
根树
如果一棵有向树,恰有一个结点的入度为$0$,其余所有结点的入度均为 $1$,则称此树为根树。
树根:入度为 $0$ 的结点。
叶:出度为 $0$ 的结点。
分支结点(内结点):出度不为 $0$ 的结点。
父结点与子结点:如果 $\langle v_i,v_j \rangle$ 是根树中的一条边,则称 $v_i$ 是 $v_j$ 的父结点,$v_j$ 是 $v_i$ 的子结点。
祖先结点与后裔结点:在根树中,如果从 $v_i$ 到 $v_j$ 有路,则称 $v_i$ 是 $v_j$ 的祖先结点,$v_j$ 是 $v_i$ 的后裔结点。
根树结点的层次:从根结点到某个结点的路径的长度,称为该结点的层次。同一层次的结点称为兄弟结点。
树高:从树根到各个叶结点的路径中,最长路径的长度,称为该树的高度(树高)。
$m$ 叉树与完全 $m$ 叉树
$m$ 叉树:在根树中,如果每个结点的出度最大是 $m$,则称此树是 $m$ 叉树。
完全 $m$ 叉树:在根树中,如果每个结点的出度都是 $m$ 或者等于 $0$,则称此树是完全 $m$ 叉树。
正则 $m$ 叉树:在完全 $m$ 叉树中,如果所有树叶的层次相同,则称之为正则 $m$ 叉树。
定理:$T$ 是棵完全 $m$ 叉树,有 $t$ 个叶结点,$i$ 个分支结点, 则 $(m – 1)i = t – 1$。
$m$ 叉有序树转化为二叉树
方法是:
- 每个结点保留左儿子结点,剪掉右边其分支。被剪掉的结点如下处理(重新嫁接)。
- 同一个层次的结点,从左到右依次画出(被剪掉的结点嫁接到它的哥哥结点上)。

最优树(哈夫曼树)
带权二叉树的定义
设有一组权值:$w_1, w_2, w_3,\cdots , w_m$,不仿设 $w_1 \le w_2 \le w_3 \le \cdots \le w_m$,设有一棵二叉树有 $m$ 片叶子,分别带有权值 $w_1, w_2, w_3, \cdots, w_m$,称此树为带权二叉树。
带权树 $T$ 的权 $W(T)$
$$
W(T) = \sum_{i = 1}^m w_i L(w_i)
$$
其中 $L(w_i)$ 是标有权 $w_i$ 的叶结点的从根到该叶结点的路长。
最优树
带权树中,权数最少的二叉树。
画最优树的算法——哈夫曼算法
- 先将权按照升序排序,设为 $w_1 \le w_2 \le w_3 \le \cdots \le w_m$。
- 以 $w_1$ 和 $w_2$ 为儿子结点,构造它们的父结点,且其权为 $w_1 + w_2$,并从权的序列中去掉 $w_1$ 和 $w_2$。
- $w_1 + w_2$ 再与其余权一起排序,再从此队列中取出前面两个权值为儿子结点,同 2 的方法构造它们的父结点。
- 依此类推,直至最后,即得到最优树。
前缀码(哈夫曼编码)
问题的提出:数据通讯时,需要将信息编码,即用二进制符号串表示信息。
前缀码定义:一个符号的编码不是另一个符号编码的前缀。
前缀码的设计:每棵二叉树一一对应一组前缀码。
平面图
平面图
定义
设 $G$ 是无向图,如果能将 $G$ 的所有结点和边都画在一个平面上,且使得任何两条边除了端点外没有其它交点,则称 $G$ 是个平面图。
画出的没有边交叉出现的图,称为 $G$ 的平图。
一个图表面上是个非平面图,如果通过改变边的位置就变成平面图,称此图是可平面化的。
定理
Jordon 曲线:一条连续的,自身不相交的,起点和终点相重合的曲线。
平面图的圈中各条边的并集构成一条 Jordon 曲线。
设 $J$ 是平面上的一条 Jordon 曲线,平面的剩下部分被分成两个不相交的开集,称为 $J$ 的内部和外部,分别记为 $\mathrm{int} J$ 和 $\mathrm{ext} J$,并且用 $\mathrm{Int} J$ 和 $\mathrm{Ext} J$ 表示它们的闭包。显然 $\mathrm{Int} J \cap \mathrm{Ext} J = J$。
Jordon 曲线定理:连接 $\mathrm{int} J$ 的点和 $\mathrm{ext} J$ 的点的任何连线必在某点和 $J$ 相交。
对偶图
平面图的面、边界及面的度数
设 $G$ 是个平面图,图中边围成的区域,其内部不含有结点,也不含有边,称这样区域为 $G$ 的一个面。
面的边界:围成一个面 $f$ 的所有边构成的回路,称之为这个 $f$ 面的边界。
此回路中的边数,称之为面 $f$ 的度数,记作 $d(f)$。
$F(G)$:平面图 $G$ 中面的集合。
$r(G) = |F(G)|$,面的个数。
对偶图的定义
给定平面图 $G = \langle V,E \rangle$,可以定义另一个图 $G^* = \langle V^*,E^* \rangle$,如下:
- 对于 $G$ 中的每个面 $f$,都有 $G^*$ 的点 $f^*$ 与之对应。
- 对于 $G$ 中的每条边 $e$,都有 $G*$ 的边 $e^*$ 与之对应。
- $G^*$ 中的点 $f^*$ 与 $g^*$ 被边 $e^*$ 相连 $\Leftrightarrow G$ 中的面 $f$ 和 $g$ 被 $e$ 分隔。
图 $G^*$ 称为图 $G$ 的对偶图。
对偶图的性质
- $G^*$ 是唯一的,且 $G^*$ 是连通的。
- $G^*$ 是平面图。
- 若 $G$ 是平面连通图,则 $(G^*)^* = G$。
- $m(G^*) = m(G),n(G^*) = r(G)$。
$d(v^*) = d(f)$。
定理:若 $G$ 是平面图,则:
$$
\sum_{f \in F} d(f) = 2m
$$
证明:即等于其对偶图边数。
欧拉公式——关于点,边和面的数目的简单公式
$G$ 是个连通的平面图,设 $n,m,r$ 分别表示 $G$ 中结点数、边数、面数,则有 $n – m + r = 2$。

推广:对任意 $p(p \ge 1)$ 个连通分支的平面图 $G$ ,有 $n – m + r = p + 1$。
推论:对任意平面图,有 $n – m + r \ge 2$。
由欧拉公式得到的推论
推论 1:若 $G$ 是 $n\ge 3$ 的简单(连通)平面图,则 $m \le 3n – 6$。
推论 2:若 $G$ 是简单连通平面图,则 $\delta \le 5$。
推论 3:$K_{3,3}$ 是非平面图。

五色定理和四色定理
相关名词
地图:没有桥的连通平面图。
地图着色:在平面或球面上的地图,为使相邻两个国家(或地区)便于区分,必须对这两个国家(或地区)着以不同的颜色,那么一个具体的区域图至少要用多少种颜色才够呢?
四色猜想:每个平面图是四面可着色的。
顶点着色
图 $G$(可以是任意的图)的正常着色(简称着色):
- $k$ 顶点着色:$k$ 种颜色对图 $G$ 的顶点的一个分配。
- $k$ 顶点着色是正常的(或 $k$ 顶点可着色),简称 $k-$ 可着色:若 $G$ 中任意两个相邻的顶点都分配到不同的颜 色。
- 对 $G$ 着色时,需要的最少颜色数,称为 $G$ 的着色数,记作 $x(G)$。
结论
- $G$ 是 $k-$ 可着色的,相当于把 $G$ 的顶点分成 $k$ 个独立集的一个分类 $(V_1, V_2, \cdots, V_k)$。
- $G$ 是 $k-$ 色的 $\Leftrightarrow G$ 的简单图是 $k-$ 色的。
- 一个简单图的 $x(G) = 1 \Leftrightarrow G$ 是空图。
- 一个简单图的 $x(G) = 2 \Leftrightarrow G$ 是二部图。
- $G$ 是完全图 $K_n$,则 $x(G) = n$。
- $G = K_n-e$,则 $x(G) = n – 1$。
- $G = C_n$,则当 $n$ 为偶数时,$x(G) = 2$;当 $n$ 为奇数时,$x(G) = 3$。
对G着色方法(介绍韦尔奇.鲍威尔法)
具体步骤:
- 将图中所有点按度数大小递减排列(此排列可能不唯一,因为可能有些结点的度数相同)。
- 用第一种颜色对第一个点(度数最大的点)着色,并且按排列顺序对与前面着色点不相邻的每个点着上同样的颜色。
- 用第二种颜色对尚未着色的点重复步骤。
- 用第三种颜色继续这种做法,直到所有的点全部着上色为止。
着色数相关的一个定理
定理:对任意图 $G$ ,有 $x(G) \le \Delta + 1$,其中 $\Delta$ 为 $G$ 中顶点的最大度。

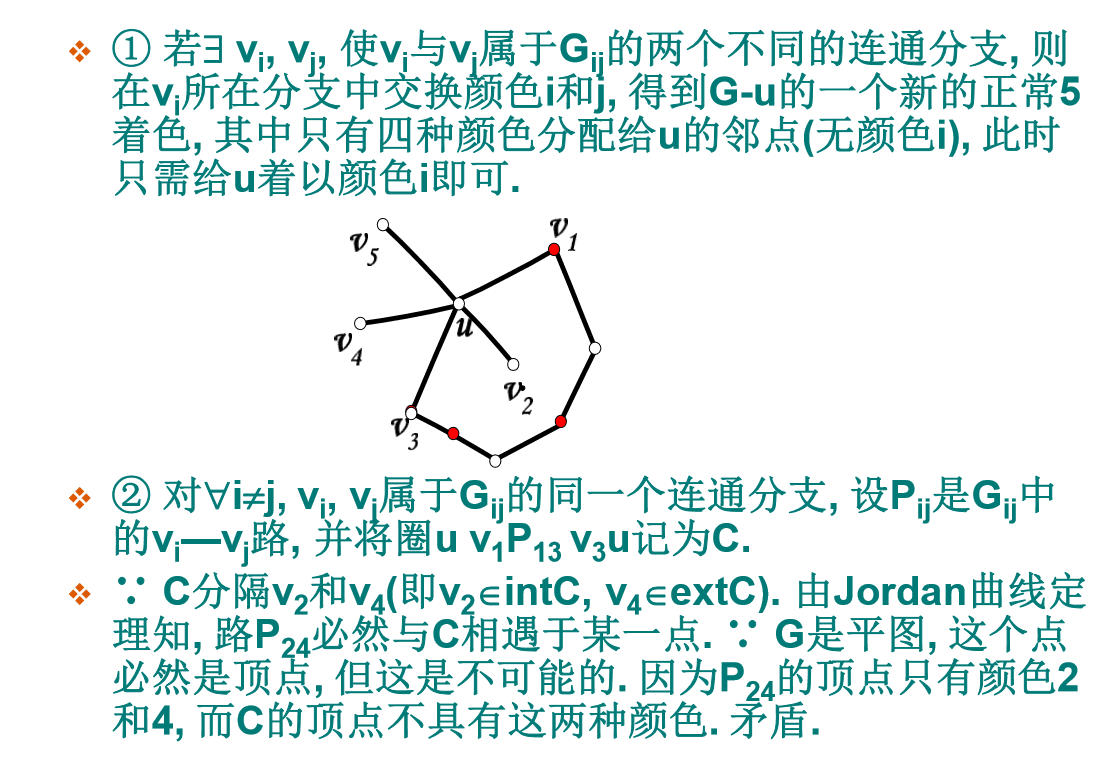
五色定理
每个平面图都是 $5$ 顶点可着色的。

面着色
$k$ 面着色:$k$ 种颜色给平面图 $G$ 的所有面的一个分配。
正常的面着色:若被一条边分隔的两个面分配以不同的颜色。
$k$ 面可着色:若 $G$ 有一个正常的 $k$ 面着色。
面色数 $x^*(G) =$ 使 $G$ 是 $k$ 面可着色的最小 $k$ 值,显然 $x^*(G) = x(G^*)$。
可以证明:每个平面图都是 $k$ 顶点可着色的 $\Leftrightarrow$ 每个平面图都是 $k$ 面可着色的。
四色定理:每个平面图是 $4$ 面可着色的。
与四色定理相关结论
定理 1:如果平面图 $G$ 有哈密顿圈,则四色猜想成立。

定理 2:连通平面图 $G$ 的面可 $2-$ 着色当且仅当 $G$ 中存在欧拉回路。

图的外可平面性(平面图的判断问题)
下面要介绍两个判定一个图是平面图的充分且必要条件,即 Kuratowski (库拉托斯基)定理。
在此之前先介绍两个新运算——插入或消去 $2$ 度点。
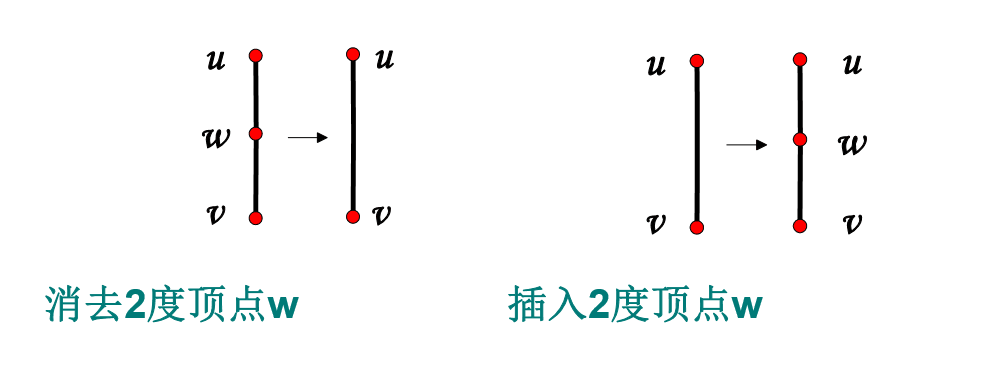
定义 1:如果两个图 $G_1$ 和 $G_2$ 同构,或经过反复插入或消去 $2$ 度顶点后同构,则称 $G_1$ 和 $G_2$ 同胚。
定义 2:图 $G$ 中相邻顶点 $u, v$ 之间的初等收缩由下面方法给出:删除边 $(u, v)$,用新的顶点 $w$ 取代 $u, v$,使 $w$ 关联和 $u,v$ 关联的一切边(除 $(u, v)$ 外)。
库拉图斯基定理:一个图是平面图,当且仅当它不包含同胚于 $K_{3,3}$ 或 $K_5$ 的子图。
另一种叙述形式:一个图是平面图,当且仅当它没有可以收缩到 $K_{3,3}$ 或 $K_5$ 的子图。



No Comments