
电子电路与系统基础笔记(3)——电容与电感
电路元件——电容与电感
电容与电感
电容
电容是对导体结构保持自由电荷能力大小的描述:
$$
C = \frac{q}{v}
$$
- 自由电荷在导体结点上积累或消散,电荷形成的空间电场随时间发生变化,这种时变电场形成位移电流:电容描述导体结构(结点)电压变化形成位移电流的大小。
$$
i(t) = \frac{\mathrm{d} q(t)}{\mathrm{d} t} = C \frac{\mathrm{d} v(t)}{\mathrm{d} t}
$$ 电容同时也是对导体结构电能存储能力大小的描述。
$$
E(t) = \frac{1}{2} C v^2(t)
$$
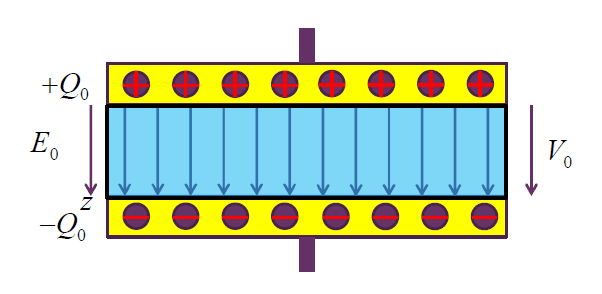
极板之间的电容:
$$
C = \frac{Q_0}{V_0} = \varepsilon \frac{S}{d}
$$
电感
电感是对导线结构流通电流产生与链接磁通能力大小的描述。
$$
L = \frac{\varphi}{i}
$$
- 导线回路有电流流过,电流产生磁场,磁场在导线平面的通量为磁通,因而电流产生磁通。当电流发生变化时,磁通发生变化,时变磁通产生感生电动势,以阻碍电流的变化:电感描述导线结构(回路)电流变化形成感生电动势的大小。
$$
v(t) = \frac{\mathrm{d} \varphi(t)}{\mathrm{d} t} = L \frac{\mathrm{d} i(t)}{\mathrm{d} t}
$$ 电感同时也是对导线结构磁能存储能力大小的描述。
$$
E = \frac{1}{2} L i^2(t)
$$
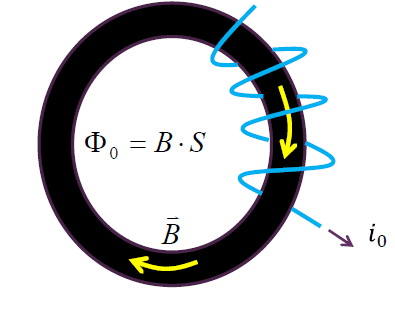
绕圈电感:
$$
L = \frac{N \Phi_0}{i_0} = \frac{NBS}{i_0} \\
= \frac{N (\mu \frac{N}{p} i_0) S}{i_0} = N^2 \mu \frac{S}{p} = N^2 \Xi
$$
磁环磁导 $\Xi = \mu \frac{S}{p}$。
电容与电感特性
记忆性
电容的端口电压是状态变量:电容电压依赖于之前所有时间段的电流,它是有记忆的。
$$
v(t + \Delta t) = v(t) + \frac{\Delta Q}{C} = v(t) + \Delta v
$$
状态变量具有的特征:当前状态由前一时刻状态转移而来,是前一状态基础上的变化。
而电阻则是无记忆元件:当前电压仅由当前电流决定,和以前的电流没有任何关系。
连续性
如果电流有界:
$$
v_C(t^+) = v_C(t^-), v_C(0^+) = v_C(t^-)
$$
则电容两端电压不会发生突变,电容电压是连续变化的。
功率与能量
电容吸收的电能,以电荷存储的形式存储在电容结构中,定义为电容储能。
而电导吸收的电能,以热能/光能等形式释放,定义为电阻耗能。
无损性
电容的释能 $=$ 吸能,故无损。
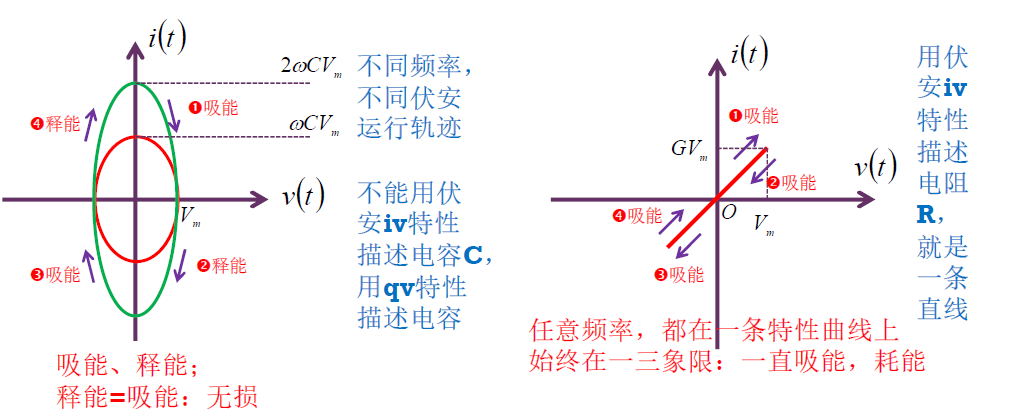
电容特性描述

微分电容

电容和电感的三个基本特性
类比电容,应用对偶即可得到电感的记忆性,连续性,无损性。
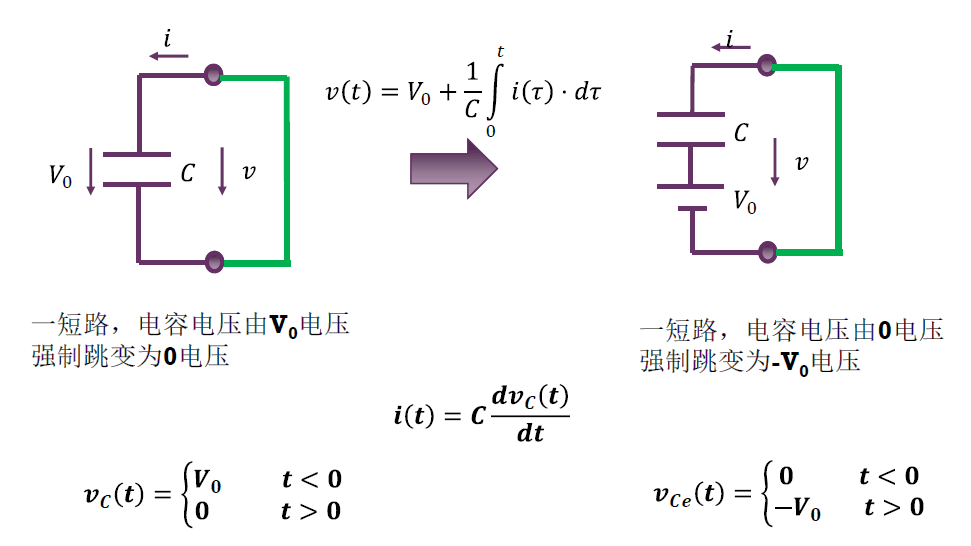
电容初始电压的源等效
电容具有初始电压,电容则可向外释放电能,因而具有初始电压的电容是有源的,其有源性如何体现?
$$
v(t) = V_0 + \frac{1}{C} \int_0^t i(\tau) \mathrm{d} \tau
$$

电容初始电压的有源性体现为和电容串联的恒压源。
戴维南等效和诺顿等效
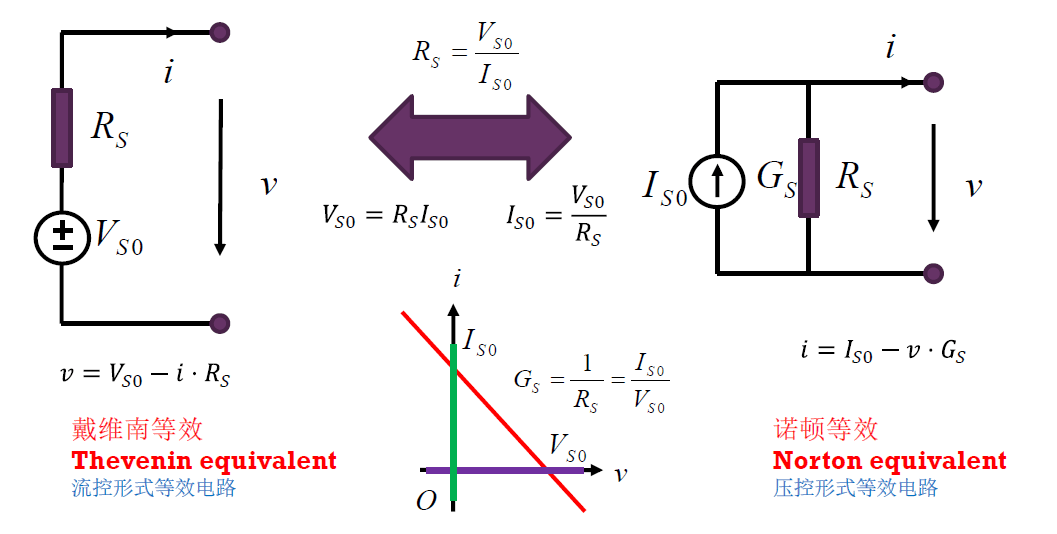
戴维南源电压为端口开路电压,诺顿源电流为端口短路电流。
有初始电压的电容的诺顿等效?
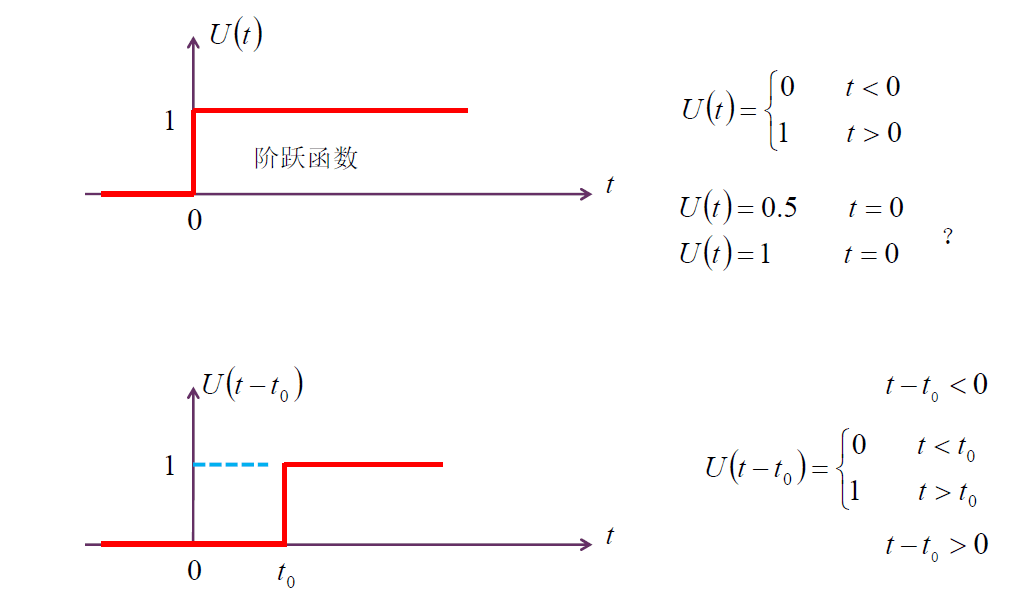
出现了跳变函数以及对跳变函数的微分。
单位阶跃函数
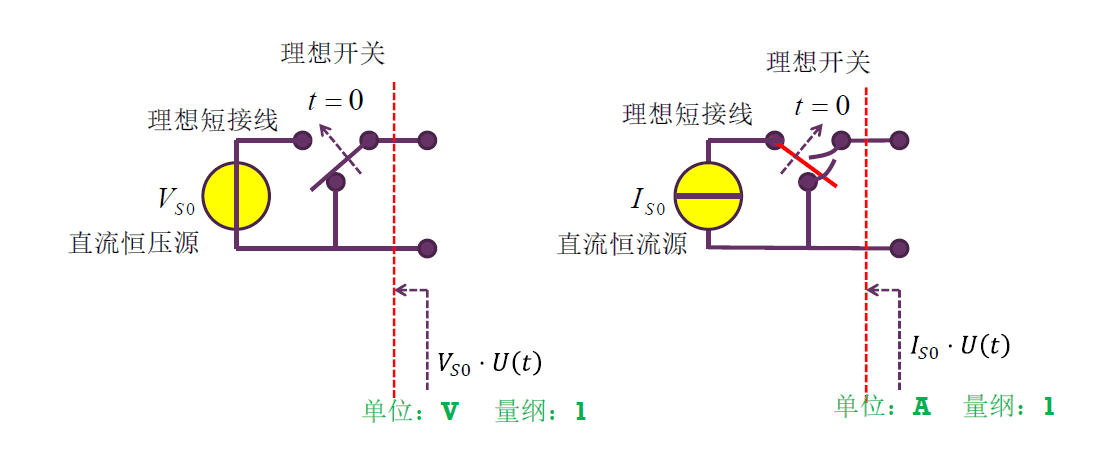
越阶信号源的电路实现
单位冲激函数
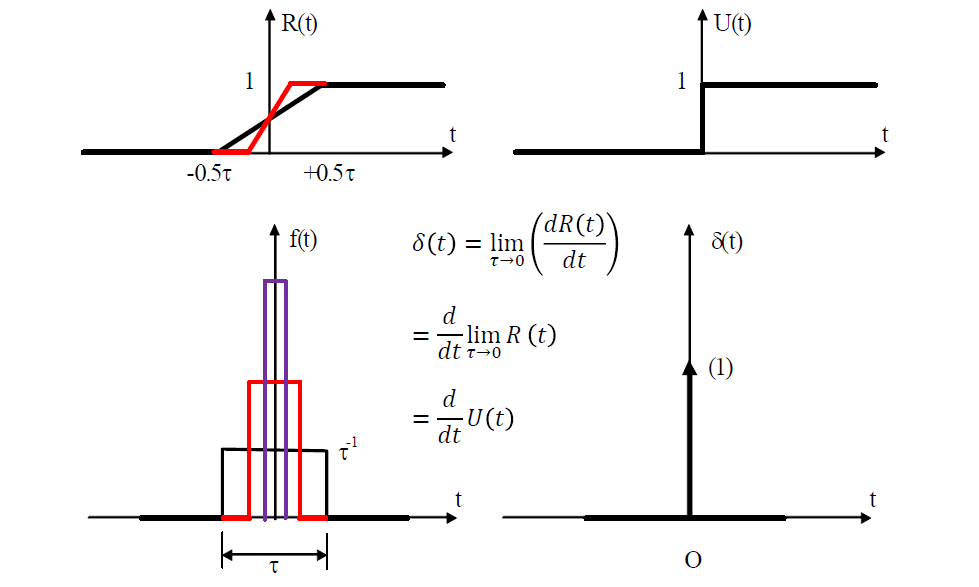
面积为 $1$,宽度为 $0$:单位冲激
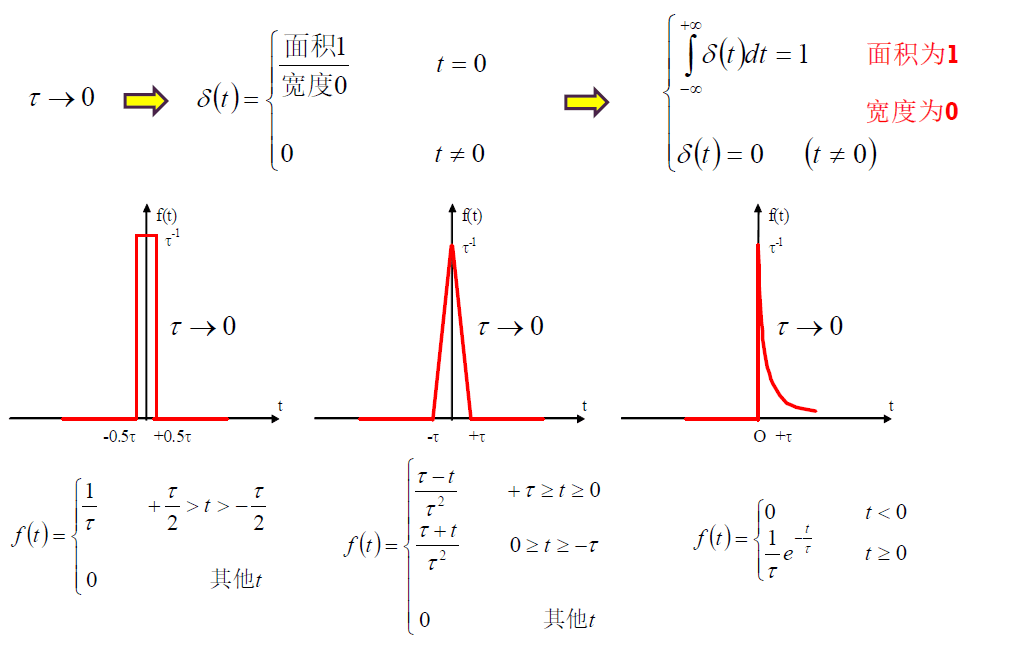
单位越阶函数量纲为 $1$,单位冲激函数量纲为 $1/s$。
冲激信号的电路数学抽象

状态跳变的可能性
如果充电电流有界,则电容电压随时间是连续变化的。
- 当存在冲激电流时,电容电压则会出现跳变。
$$
v_C(t_0^+) – v_C(t_0^-) = \frac{1}{C} \int_{t_0^-}^{t_0^+} i_C(\tau) \mathrm{d} \tau = V_0 U(t – t_0)_{t = t_0^+} = V_0 \\
i_C(t) = C V_0 \delta(t – t_0)
$$
如果充磁电压有界,则电感电流随时间是连续变化的。
- 当存在冲激电压时,电感电流则会出现跳变。
$$
i_L(t_0^+) – i_L(t_0^-) = \frac{1}{L} \int_{t_0^-}^{t_0^+} v_L(\tau) \mathrm{d} \tau = I_0 U(t – t_0)_{t = t_0^+} = I_0 \\
v_L(t) = L I_0 \delta(t – t_0)
$$
有初始电压的电容的诺顿等效电路
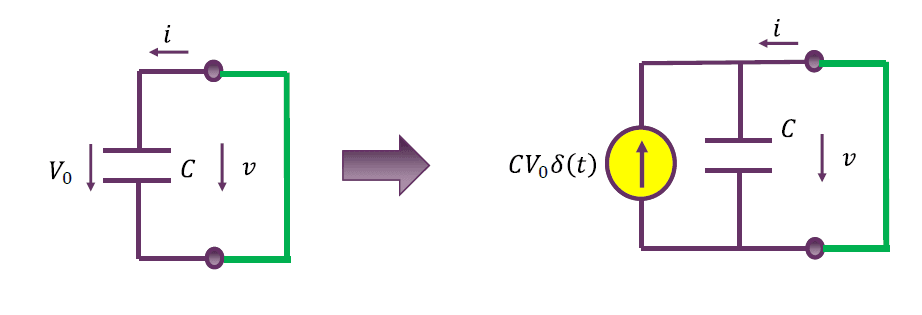
$$
v_C(t) =
\begin{cases}
V_0 & t < 0 \\
0 & t > 0
\end{cases}
= V_0 (1 – U(t))
$$
端口短路电流:
$$
i(t) = C \frac{\mathrm{d}}{\mathrm{d} t} v_C(t) = -C V_0 \delta(t)
$$
具有初始电压的电容的等效电路
一旦考虑初始电压,就有起始时间点的限制:$t \ge 0$。
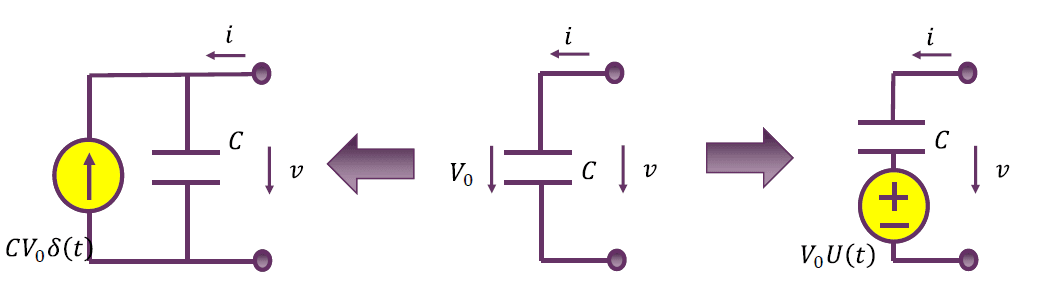
未考虑初始电压元件约束:
$$
i(t) = C \frac{\mathrm{d}}{\mathrm{d} t} v(t) \\
v(t) = V_0 + \frac{1}{C} \int_0^t i(\tau) \mathrm{d} \tau, t \ge 0
$$
考虑初始电压的元件约束,仅 $t \ge 0$ 时成立:
$$
i(t) = -C V_0 \delta(t) + C \frac{\mathrm{d}}{\mathrm{d} t} v(t) \\
v(t) = V_0 U(t) + \frac{1}{C} \int_0^t i(\tau) \mathrm{d} \tau
$$
具有初始电流的电感的等效电路
一旦考虑初始电压,就有起始时间点的限制:$t \ge 0$。
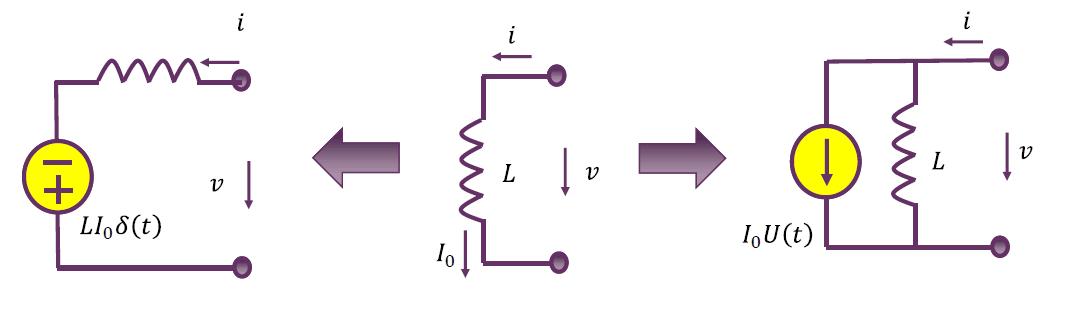
未考虑初始电压元件约束:
$$
v(t) = L \frac{\mathrm{d}}{\mathrm{d} t} i(t) \\
i(t) = I_0 + \frac{1}{L} \int_0^t v(\tau) \mathrm{d} \tau, t \ge 0
$$
考虑初始电压的元件约束,仅 $t \ge 0$ 时成立:
$$
v(t) = -L I_0 \delta(t) + L \frac{\mathrm{d}}{\mathrm{d} t} i(t) \\
i(t) = I_0 U(t) + \frac{1}{L} \int_0^t v(\tau) \mathrm{d} \tau
$$
电容/电感串并联
电容并联

$$
i = (\sum_{k = 1}^n C_k) \frac{\mathrm{d} v}{\mathrm{d} t} = C \frac{\mathrm{d} v}{\mathrm{d} t} \\
C = \sum_{k = 1}^n C_k
$$
电容串联
假设电容无初始电压。
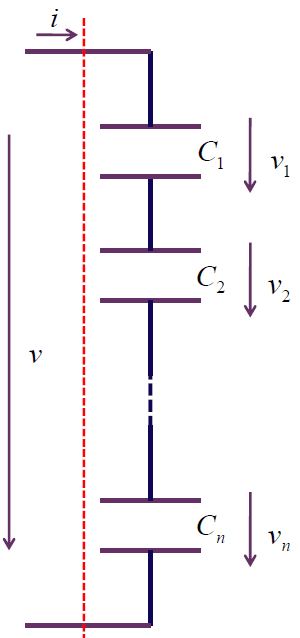
$$
v = \sum_{k = 1}^n v_k = \sum_{k = 1}^n \frac{1}{C_k} \int_0^t i \mathrm{d} t \\
= (\sum_{k = 1}^n \frac{1}{C_k}) \int_0^t i \mathrm{d} t \\
= \frac{1}{C} \int_0^t i \mathrm{d} t \\
\frac{1}{C} = \sum_{k = 1}^n \frac{1}{C_k}
$$
即电容和电导的串并联公式形式一致。
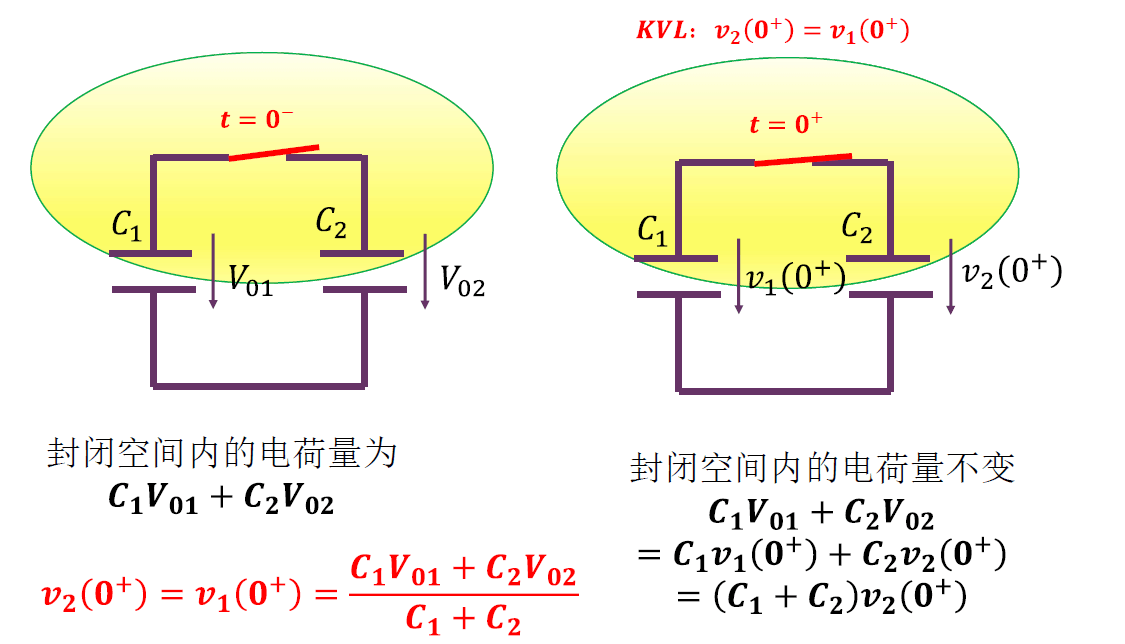
有初始电压的电容串联
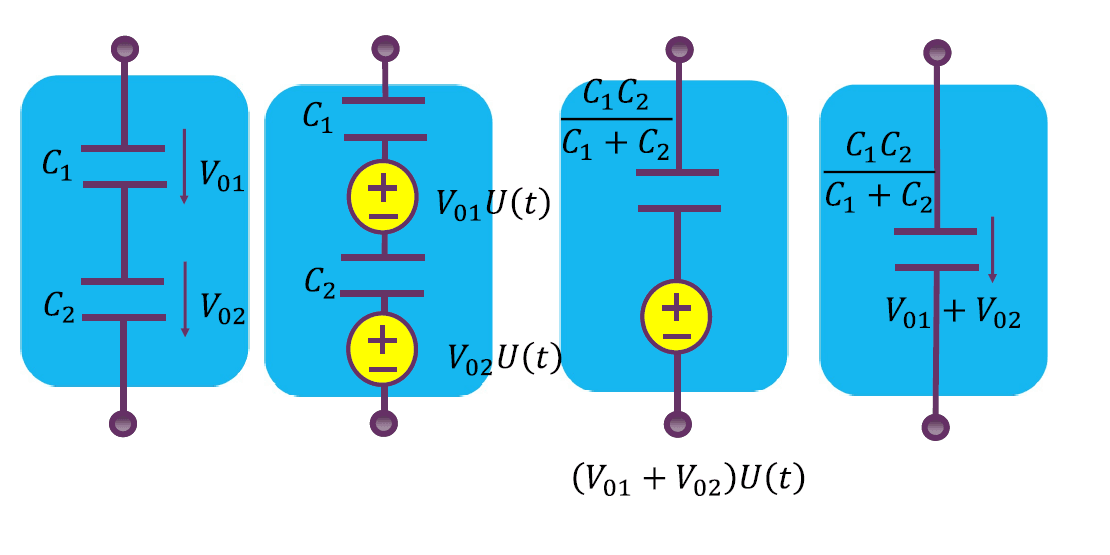
有初始电压的电容并联
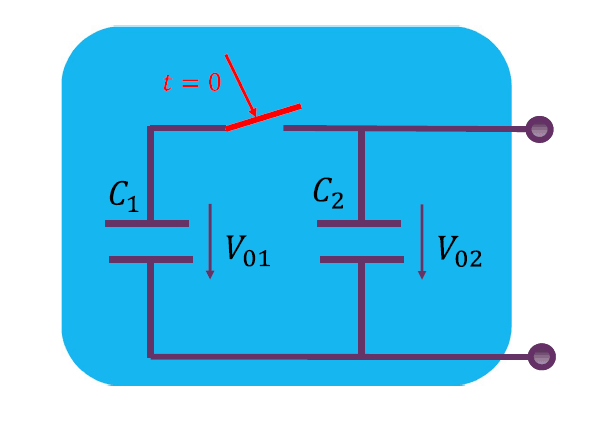
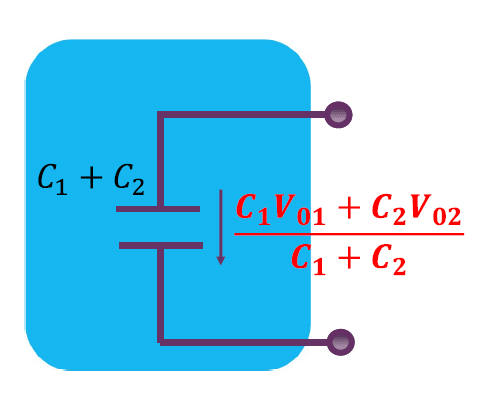
总结
串联用戴维南源等效:压加压,阻加阻;
并联用诺顿源等效:流加流,导加导。
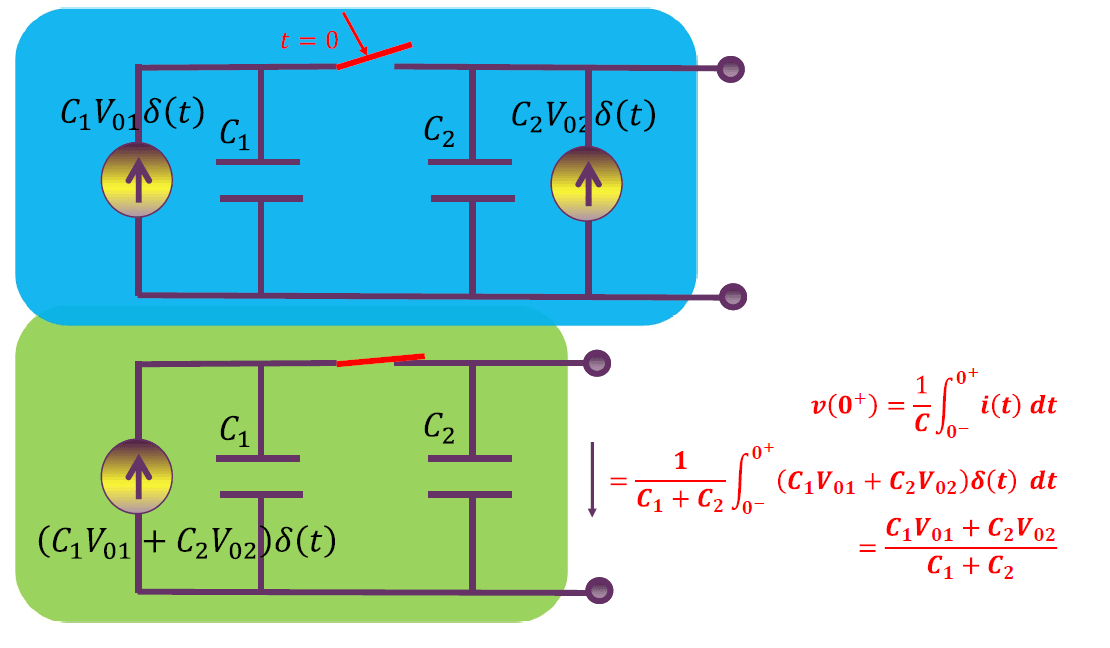
另外一种理解:电荷守恒
例 1:正弦波电流源驱动电容
$$
v(t) = V_0 + \frac{1}{C} \int_0^t i(\tau) \mathrm{d} \tau \\
= V_0 + \frac{I_p}{\omega C} \sin \omega t
$$
$\omega C$ 具有电导的 $S$ 量纲,被称为电纳,和电导一并统称为导纳;后面讨论时,言导纳多于言电导。
对交流而言,电容是高频短路的。
当频率极高时,电容相当于直流恒压源。
例 2:正弦波电流源驱动电感
$$
i(t) = I_0 + \frac{1}{L} \int_0^t v(\tau) \mathrm{d} \tau \\
= I_0 + \frac{V_p}{\omega L} \sin \omega t
$$
$\omega L$ 具有电阻的 $\Omega$ 量纲,被称为电抗,和电阻一并统称为阻抗;后面讨论时,言阻抗多于言电阻。
对交流而言,电感是高频开路的。
当频率极高时,电感相当于直流恒流源。
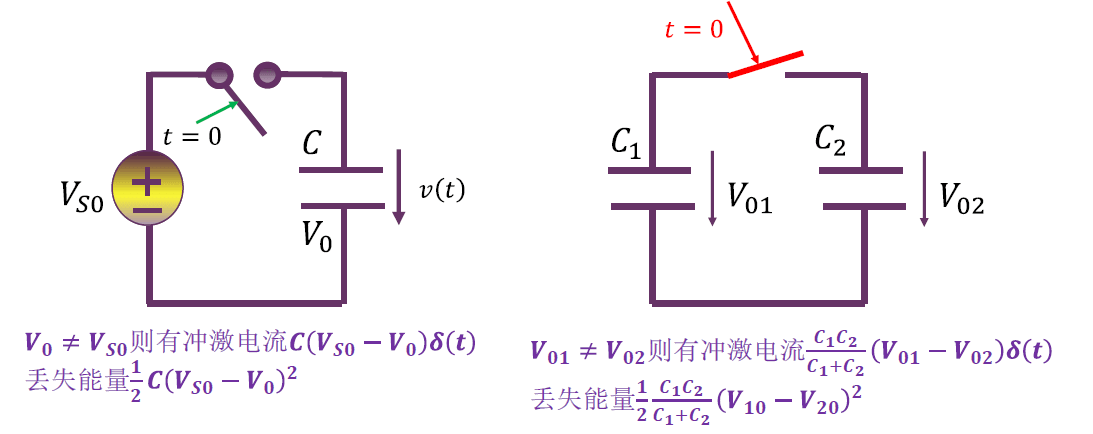
例 3:直流电压源驱动电容
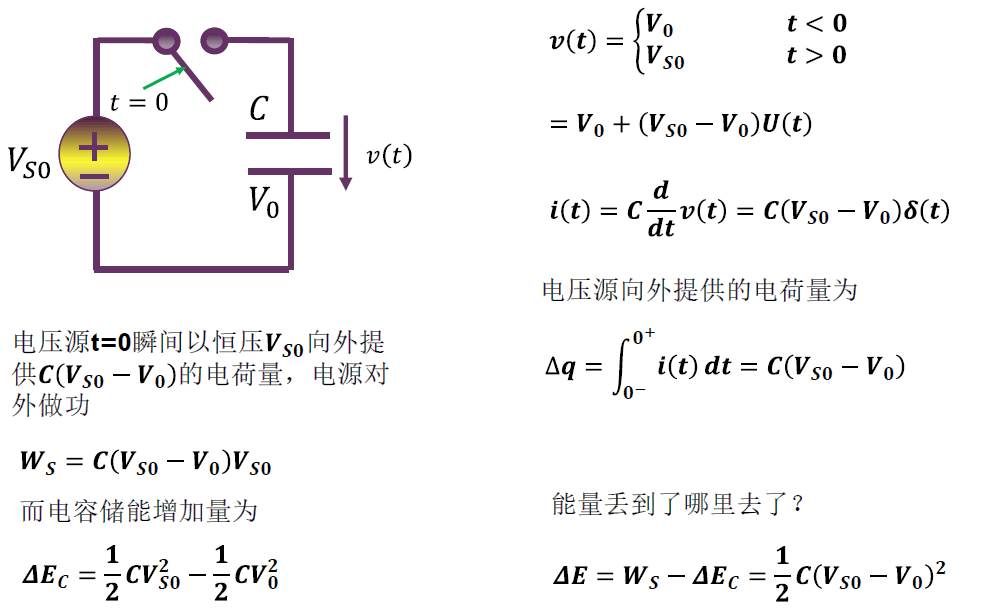
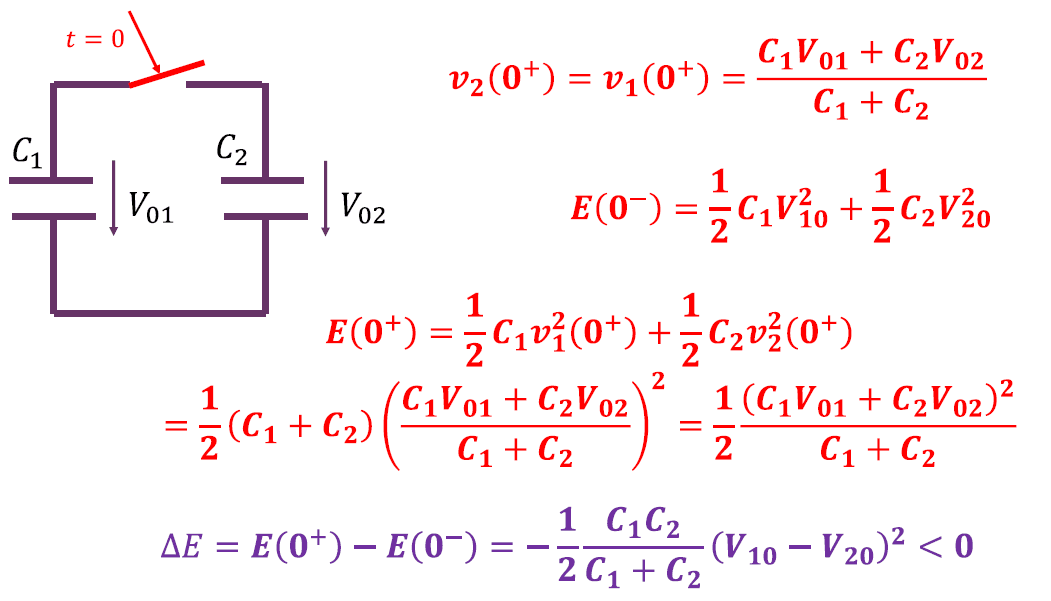
凡是有冲激信号的,能量都有丢失!
电容电压突变(有冲激电流),电感电流突变(有冲激电压),均可发现有能量丢失现象。
小结
- 电容电感是对偶元件。
- 电容电感三个基本特性:记忆性,连续性,无损性。
- 具有初始电压的电容、具有初始电流的电感是有源的,可用戴维南形式或诺顿形式表述。
- 在有界电流假设下,电容电压连续变化;在有界电压假设下,电感电流连续变化。
- 电容电压突变,说明电容电流出现冲激;电感电流突变,说明电感电压出现冲激。
- 电路中出现冲激时,从电路角度分析,存在能量丢失问题。



No Comments