
Verilog 学习笔记(6)——Verilog 语言基础(4)
组合逻辑
数字系统需要对数字信号进行处理,而处理的过程中根据对于信号是否具有记忆功能,可以将数字电路分成两类。一类电路没有记忆功能,输出直接由当时输入确定,称为组合逻辑电路(Combinational Logic Circuit).另一类具有记忆功能,输出同时与当时的输入与之前信号的历史有关,称为时序逻辑电路(Sequential Logic Circuit).(和之前提到的阻塞和非阻塞赋值也有关系).本节主要介绍组合逻辑。
卡诺图
对卡诺图做个稍微简略的介绍。
对输入变量按二进制码排列,写出输出变量,可以得到一个逻辑函数的真值表。若有两行的输入变量只有一个发生变化,则称这两项是相邻的。卡诺图就是将相邻的项在矩阵中也相邻排列,这样若相邻的项都输出1,即发生改变的输入变量对输出无影响,因此就可以将相邻的项合并,从而达到化简逻辑函数的效果。如图所示(这个课本版本扫描质量较差将就着看)。
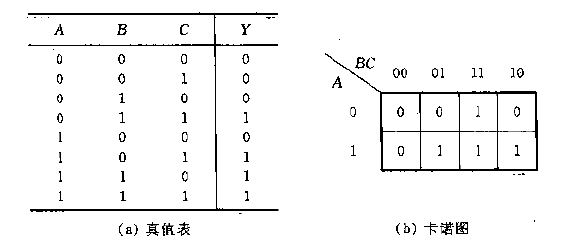
图(b)中可以合并的项的 ABC 编码为 (101,111), (011,111), (110,111),我们将可以合并的项画到一个圈里,每个圈就是一项,画圈后的卡诺图如图所示。
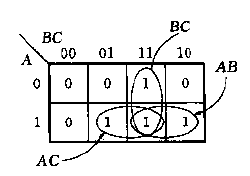
也就是说一个最小项为
$$
Y=\overline{A}BC+A\overline{B}C+AB\overline{C}+ABC
$$
的逻辑函数可以化简为
$$
Y=AC+BC+AB
$$
卡诺图化简有几个注意的地方:
- 卡诺圈必须包含了所有最小项(即图中所有1)
- 卡诺圈只能是 1*1,1*2,2*2,2*4,4*4 (一般卡诺图最大画到4*4,因为再大的卡诺图无法保证全部相邻)
- 卡诺图最左和最右是相邻的,最上和最下是相邻的
此外卡诺图还有一些特殊的操作比如阻塞法或者异或化简不作介绍,感兴趣的可以自己了解。
组合逻辑电路分析
组合逻辑电路一般是单向的信号并有确定的逻辑函数,因此只需要根据其逻辑关系逐级分析下来即可。当电路较为复杂的时候可以将其模块化逐级分析。当给出一个实际的电路图时只要有耐心捋顺所有电路模块的逻辑关系,就可以很轻松地通过连续赋值语句描述电路,这里就不举例子了。
关键在于:
- 将电路模块化
- 写出各级输出与输入信号的逻辑关系
- 化简逻辑函数
- 用连续赋值语句搭建电路模块
组合电路设计
设计没啥好说的,根据需要的需求分析电路的功能,确定输入信号和输出信号。考虑输入信号和输出信号的逻辑关系,通过连续赋值语句描述(当然有的时候通过行为描述也可能更简单比如选择器)。
e.g.1
假设你正在设计一个电路来控制手机的振铃器和振动电机。当手机来电时(input ring),电路必须把震动( output motor = 1 )或响铃( output ringer = 1 )打开,但不能同时打开。当手机处于震动模式时( input vibrate = 1 ),则打开震动( output motor = 1 )。否则打开响铃。
模块端口如下:
module top_module (
input ring,
input vibrate_mode,
output ringer, // Make sound
output motor // Vibrate
);
解:
乍一看这种模式的题目像是一个分支判断的问题,如果软件编程编多了可能就会像我当时一样直接上 always 块 if 语句然后遭重 QAQ。
always@(*)
if(vibrate_mode&ring)
begin
motor=1;
ringer=0;
end
else if(ring)
begin
motor=0;
ringer=1;
end
else
begin
motor=0;
ringer=0;
end
实际上硬件编程要转变思考方式,考虑在一个输出下输入分别是哪些情况。
显然,只有当 ring 和 vibrate_mode 信号都为1时才会打开震动,只有 ring 为1,vibrate_mode 信号为0时才会响铃,因此逻辑函数很容易写出来。只需要简单的连续赋值语句就可以完成这个电路。
module top_module (
input ring,
input vibrate_mode,
output ringer, // Make sound
output motor // Vibrate
);
assign ringer=ring&(!vibrate_mode);
assign motor=ring&vibrate_mode;
endmodule
e.g.2
超前进位加法器
在结构化描述一节中留了一道思考题,设计超前进位加法器。这里以四位全加器为例分析一下。
首先构建一位全加器的基本模块,这个比较简单。
module adder_1(
input a,
input b,
input cin,
output sum,
output cout
);
assign {cout,sum} = a+b+cin;
endmodule
问题在于下一级的进位输入需要前一级的进位输出才能进行运算,即整个电路是一级一级延迟传递的。为了避免这个延迟,是否存在将高位进位直接用输入表示的方法就是超前进位加法器所要考虑的。
令第 $i$ 级的进位输出为 $C_i$,那么有
$$
C_i=A_iB_i+A_iC_{i-1}+B_iC_{i-1}=A_iB_i+(A_i+B_i)C_{i-1}
$$
这样我们就得到了进位的迭代关系式,令$AB=P$,$A+B=Q$,可以得到前四级的进位输出为
$$
C_0=P_0+Q_0C_{-1}\\
C_1=P_1+Q_1C_{0}=P_1+Q_1(P_0+Q_0C_{-1})=P_1+P_0Q_1+Q_0Q_1C_{-1}\\
C_2=P_2+P_1Q_2+P_0Q_1Q_2+Q_0Q_1Q_2C_{-1}\\
C_3=P_3+P_2Q_3+P_1Q_2Q_3+P_0Q_1Q_2Q_3+Q_0Q_1Q_2Q_3C_{-1}
$$
将一位全加器的基本模块稍作修改以得到 $P,Q$ 的输出,
module adder_1(
input a,
input b,
input cin,
output P,
output Q,
output sum
);
assign sum=a^b^cin;
assign P=a&b;
assign Q=a|b;
endmodule
分析超前进位电路模块的端口,这个模块的功能是通过各级的输入直接计算出最高位的输出,因此输入端口为位宽四位的 $P,Q$,以及进位输入 $cin$.输出为各级进位输出 $cout$ .
module cpg(
input [3:0] P,
input [3:0] Q,
input cin,
output [3:0] cout
);
assign cout[0]=P[0] | Q[0]&cin;
assign cout[1]=P[1] | Q[1]&P[0] | Q[1]&Q[0]&cin;
assign cout[2]=P[2] | Q[2]&P[1] | Q[2]&Q[1]&P[0] | Q[2]&Q[1]&Q[0]&cin;
assign cout[3]=P[3] | Q[3]&P[2] | Q[3]&Q[2]&P[1] | Q[3]&Q[2]&Q[1]&P[0] | Q[3]&Q[2]&Q[1]&Q[0]&cin;
endmodule
通过结构化描述将四个一位全加器和一个超前进位电路组合就可以得到四位超前进位全加器。
module adder_4(
input [3:0] a,
input [3:0] b,
input cin,
output [4:0] sum
);
wire [3:0] P,Q;
wire [2:0] cout;
adder_1 adder0(
.a(a[0]),
.b(b[0]),
.cin(cin),
.P(P[0]),
.Q(Q[0]),
.sum(sum[0])
);
adder_1 adder1(
.a(a[1]),
.b(b[1]),
.cin(cout[0]),
.P(P[1]),
.Q(Q[1]),
.sum(sum[1])
);
adder_1 adder2(
.a(a[2]),
.b(b[2]),
.cin(cout[1]),
.P(P[2]),
.Q(Q[2]),
.sum(sum[2])
);
adder_1 adder3(
.a(a[3]),
.b(b[3]),
.cin(cout[2]),
.P(P[3]),
.Q(Q[3]),
.sum(sum[3])
);
cpg cpg1(
.P(P),
.Q(Q),
.cin(cin),
.cout({sum[4],cout[3:0]})
);
endmodule
提供一个 testbench.
`timescale 1ns/1ns
module adder_4_tb();
reg [3:0] A;
reg [3:0] B;
wire [4:0] sum;
initial begin
A = 0;
B = 0;
#10;
A = 4'b0110;
B = 4'b1010;
#10;
A = 4'd3;
B = 4'd7;
#10;
A = 5;
B = 8;
#10;
A = 4'he;
B = 4'ha;
#10;
A = 4'hf;
B = 4'hf;
end
//initial begin
// #100 $finish;
//end
adder_4 adder0(
.a(A),
.b(B),
.cin(1'b0),
.sum(sum)
);
endmodule
功能仿真效果如图

有条件的话以后可能会补上时序仿真的情况以对照延时。
思考题
请设计一个有选择信号的四位加减法器,由选择信号决定加法运算还是减法运算
要求:使用结构化模块和逻辑门,而不是直接sel?a+b:a-b



Comments: 1
时隔一年来看,当时的我怎么这都会啊
狂哭,眼泪狂流