
Verilog 学习笔记(7)——应用:线性进位选择加法器
应用:线性进位选择加法器
基本原理
一个基本的一位全加器可以用下图所示模块表示
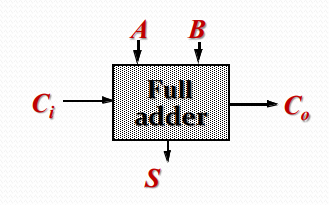
$A,B$ 为两个输入,$C_i$ 为上一级进位输入,$S$ 为该位和,$Co$ 为进位输出。
显然有以下逻辑关系
$$
S=A\oplus B\oplus C\\
C_o=AB+BC_i+AC_i
$$
简单地将多个全加器级联,就可以组成基本的脉动进位加法器,如下图
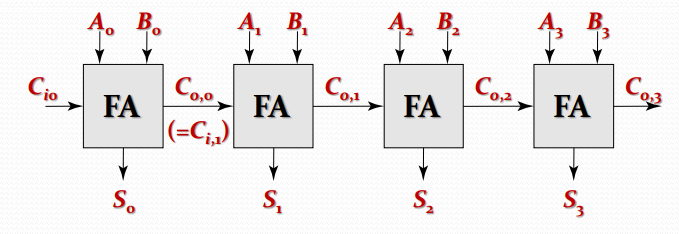
该加法器的问题在于每一级的进位运算都需要等待上一级的进位运算完毕后的进位输入,所以延时是与进位数目成线性比例的。最坏情况下,延时
$$
t_{adder}=(N-1)t_{carry}+t_{sum}
$$
其中 $t_{adder}$ 为加法器延时,$N$ 为总位数,$t_{carry}$ 指 $C_i$ 到 $C_o$ 的传输延时,$t_{sum}$ 指 $C_i$ 到 $C_o$ 的传输延时。(这里没有考虑 $t_{setup}$ )
为了解决这个问题进行优化,考虑到每级的进位只有 0 或 1 两种可能,可以先根据输入将每级在进位输入为 0 和 进位输入为 1 两种情况的输出都先运算出来,那么在进位输入之后只需要进行一次选择运算就可以得到该级输出,各级的加法运算可以并行进行,大大节省了运算时间,不过占用了更多运算资源,需要更大的面积,功耗也更大。
当每级的位数相同时,该进位选择加法器为线性进位加法器
以一个 16 位,每级 4 位的线性进位选择加法器为例,框图如下,
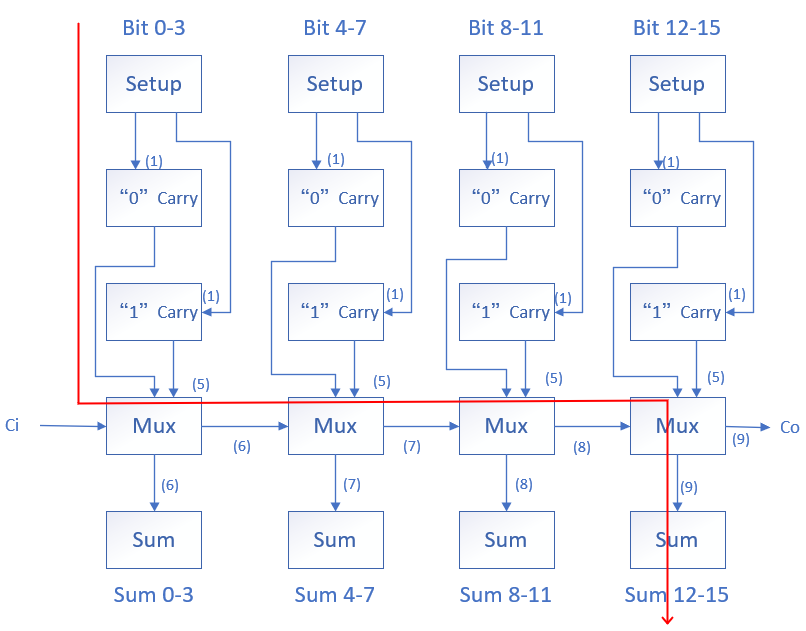
主要路径用红色箭头标出,根据框图,假定一共有 N 位,每级 M 位(N 若不是 M 的倍数则补到整数倍),可以得到最坏情况下延迟为
$$
t_{adder}=t_{setup}+M\cdot t_{carry}+N/M \cdot t_{mux}+t_{sum}
$$
Verilog 部分
按级考虑,每级需要一个 4 位默认进位输入 0 的全加器,一个 4 位默认进位输入 1 的全加器,再对两个模块的输出根据进位输入进行选择。最后将 4 个 4 位进位选择加法器级联得到 16 位线性进位选择加法器。
进位输入为 0 的 4 位全加器
module adder4_c0(
input [3:0] a,
input [3:0] b,
output [4:0] sum
);
assign sum=a+b;
endmodule
进位输入为 1 的 4 位全加器
module adder4_c1(
input [3:0] a,
input [3:0] b,
output [4:0] sum
);
assign sum=a+b+1;
endmodule
单级 4 位进位选择加法器
module adder4(
input [3:0] a,
input [3:0] b,
input cin,
output [3:0] sum,
output cout
);
wire [4:0] sum0,sum1;
adder4_c0 a0(
.a(a),
.b(b),
.sum(sum0)
);
adder4_c1 a1(
.a(a),
.b(b),
.sum(sum1)
);
assign {cout,sum}=cin?sum1:sum0;
endmodule
16 位线性进位选择加法器 (top_module)
module adder16(
input [15:0] a,
input [15:0] b,
input cin,
output [15:0] sum,
output cout
);
wire [2:0] cp;
adder4 a0(
.a(a[3:0]),
.b(b[3:0]),
.cin(cin),
.sum(sum[3:0]),
.cout(cp[0])
);
adder4 a1(
.a(a[7:4]),
.b(b[7:4]),
.cin(cp[0]),
.sum(sum[7:4]),
.cout(cp[1])
);
adder4 a2(
.a(a[11:8]),
.b(b[11:8]),
.cin(cp[1]),
.sum(sum[11:8]),
.cout(cp[2])
);
adder4 a3(
.a(a[15:12]),
.b(b[15:12]),
.cin(cp[2]),
.sum(sum[15:12]),
.cout(cout)
);
endmodule
testbench
对各级之间的进位传递进行检验,每级进位传递存在 0 ,1 两种情况,故共有 $2^4$ 个测试点,为
| A | B | 进位 |
|---|---|---|
| 0000 | 0000 | 0000 |
| eeef | 0001 | 0001 |
| ddfd | 0010 | 0010 |
| ddfe | 0002 | 0011 |
| cdcc | 0300 | 0100 |
| cdcb | 0305 | 0101 |
| cdfd | 0210 | 0110 |
| cdfe | 0202 | 0111 |
| a000 | 6111 | 1000 |
| aeef | 6001 | 1001 |
| 9dfd | 7010 | 1010 |
| 8dfe | 8002 | 1011 |
| 8dcc | 7300 | 1100 |
| 8dcc | 7304 | 1101 |
| 8dfd | 7210 | 1110 |
| 8dfe | 7202 | 1111 |
(16 进制表示)
讨论了每级进位传递为 0 和 1 的所有情况,并且讨论了各位进位为 1+f – 8+8 的所有情况
A,B 结构上对称,故不再对换进行测试
`timescale 1ns/1ps
module adder_tb();
reg [15:0] A;
reg [15:0] B;
wire [16:0] sum;
initial begin
A = 0;
B = 0;
#10;
A = 16'heeef;
B = 16'h0001;
#10;
A = 16'hddfd;
B = 16'h0010;
#10;
A = 16'hddfe;
B = 16'h0002;
#10;
A = 16'hcdcc;
B = 16'h0300;
#10;
A = 16'hcdcb;
B = 16'h0305;
#10
A = 16'hcdfd;
B = 16'h0210;
#10
A = 16'hcdfe;
B = 16'h0202;
#10
A = 16'ha000;
B = 16'h6111;
#10
A = 16'haeef;
B = 16'h6001;
#10
A = 16'h9dfd;
B = 16'h7010;
#10
A = 16'h8dfe;
B = 16'h8002;
#10
A = 16'h8dcc;
B = 16'h7300;
#10
A = 16'h8dcc;
B = 16'h7304;
#10
A = 16'h8dfd;
B = 16'h7210;
#10
A = 16'h8dfe;
B = 16'h7202;
end
adder16 adder0(
.a(A),
.b(B),
.cin(1'b0),
.sum(sum[15:0]),
.cout(sum[16])
);
endmodule
测试波形结果
功能仿真结果
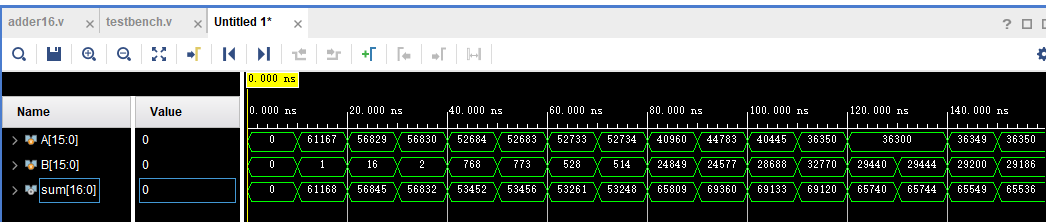
时序仿真结果
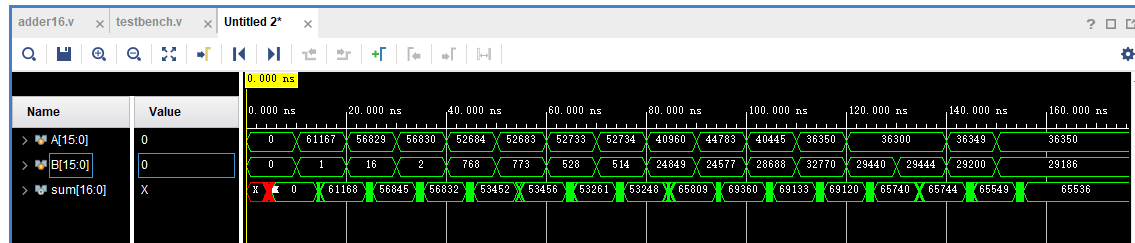
在输出发生改变的过程中会有多次反转导致出现预期外的结果,但当一定时间后仍能得到稳定正确的输出结果,说明该 16 位线性进位选择加法器并没有发生时序违规。该仿真仅是 RTL 级,仅供参考验证结构正确性。
功耗报告
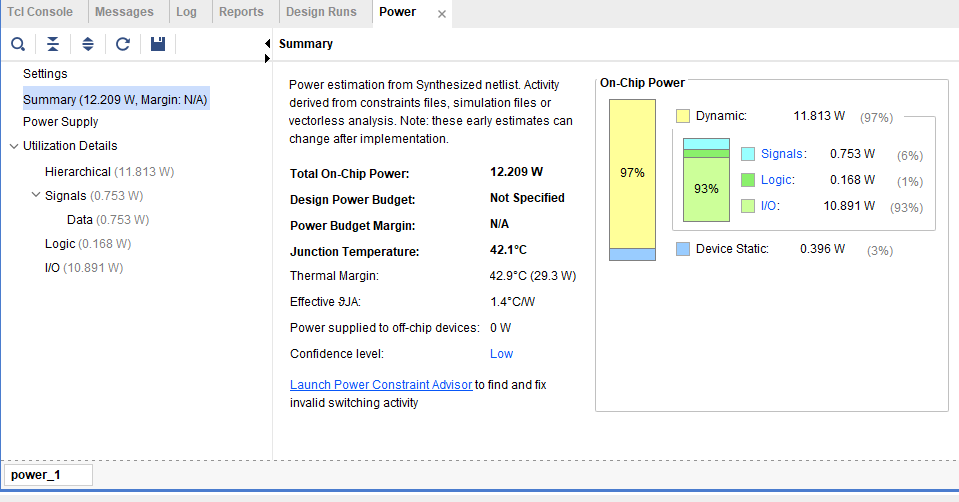



Comments: 1
功耗看个乐,显然有点离谱了