电子电路与系统基础笔记（7）——时频分析

wzf2000
2020年4月12日

电子电路与系统基础笔记（7）——时频分析

时频分析

正弦激励

回顾

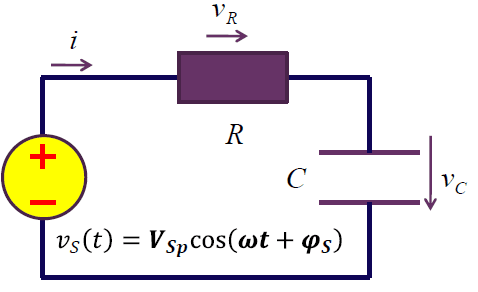
从二端口网络视角看分压

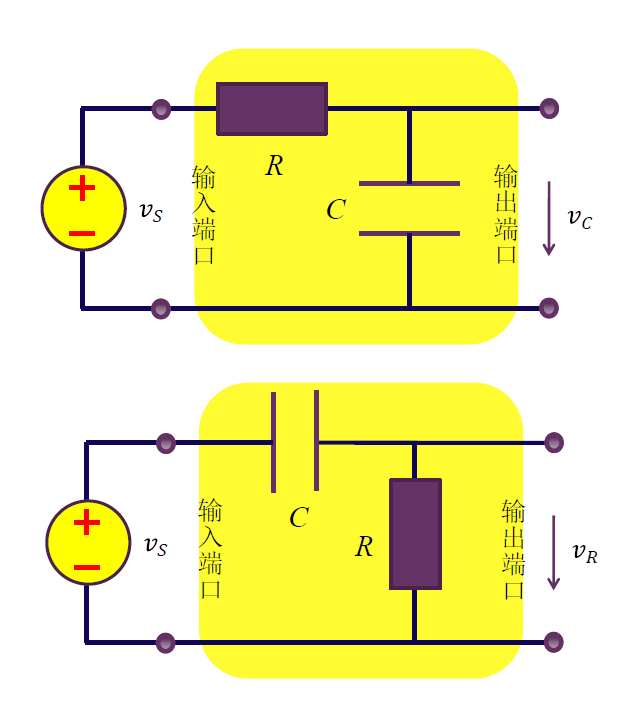
二端口网络

二端口网络是电路中最常见的网络。

• 单入单出信号处理系统的基本模型。
• 一个输入端口，一个输出端口：激励信号或能量自输入端口进入，经二端口网络处理后自输出端口输出，形成对后级的激励。
• 不做特别说明时，一般默认端口 $1$ 为输入端口，端口 $2$ 为输出端口。

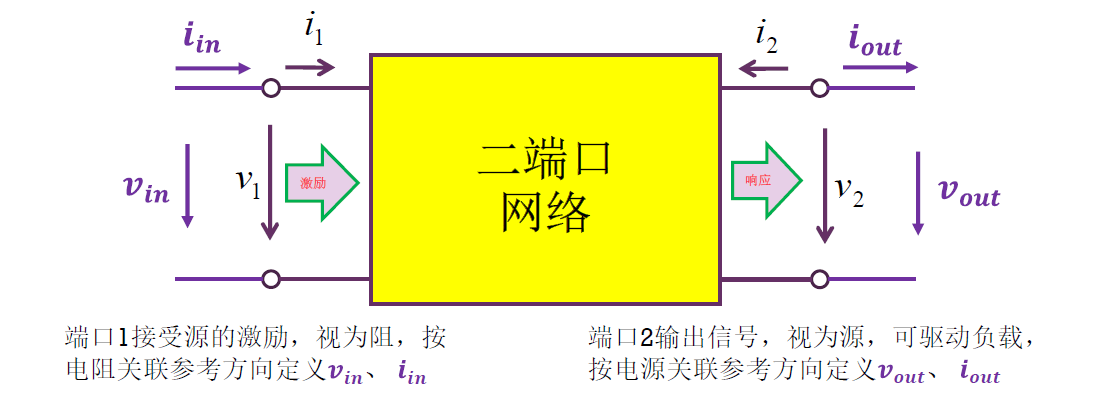
线性时不变网络（LTI）的传递函数

对二端口网络最感兴趣的参量是传递函数：
$$
H = \frac{\overset{\cdot}{S}_{out}}{\overset{\cdot}{S}_in}
$$
一般是相量域定义的传递函数。

从放大器角度称传递函数为增益（或放大倍数）。

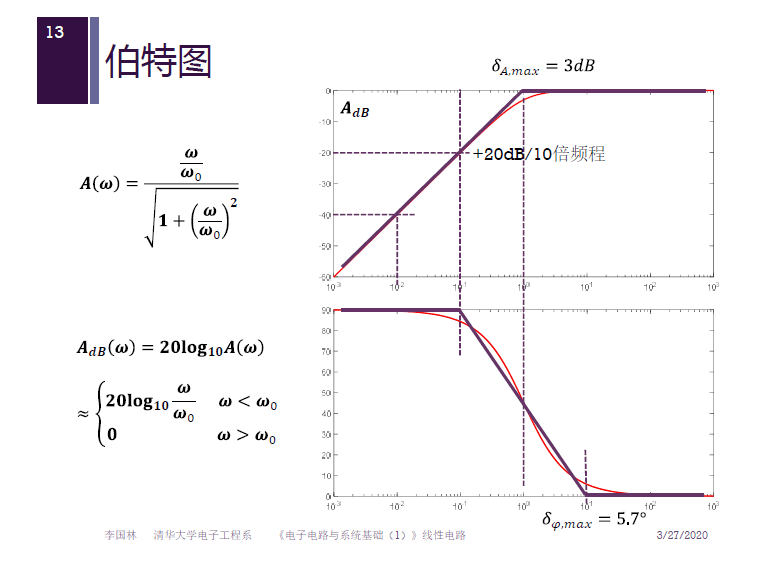
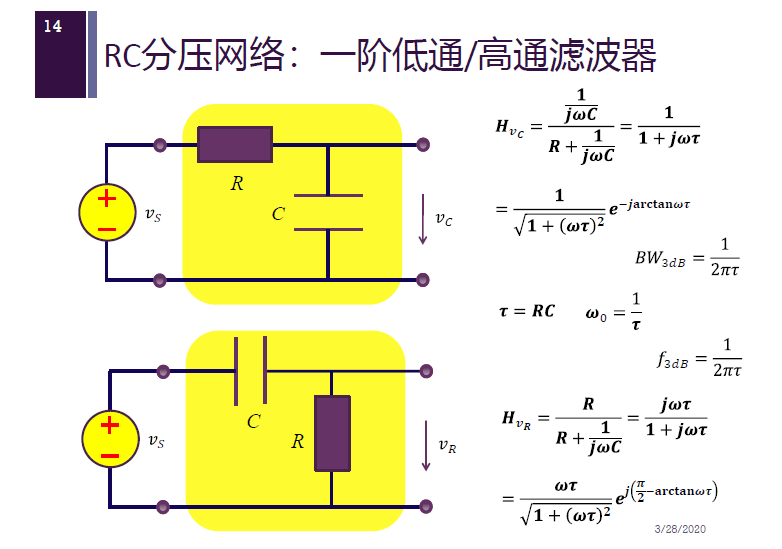
RC 分压网络的电压传递函数

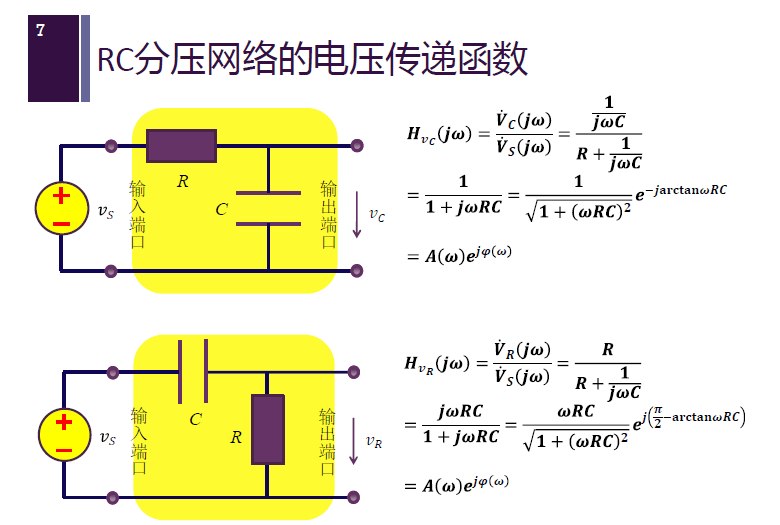
传递函数的幅频特性和相频特性

对于电容分压：
$$
A(\omega) = \frac{1}{\sqrt{1 + (\omega RC)^2}} \\
\varphi(\omega) = - \arctan \omega RC
$$

其中 $\omega_0 = \dfrac{1}{\tau} = \dfrac{1}{RC}$。

对于电阻分压：
$$
A(\omega) = \frac{\omega RC}{\sqrt{1 + (\omega RC)^2}} \\
\varphi(\omega) = \frac{\pi}{2} - \arctan \omega RC
$$

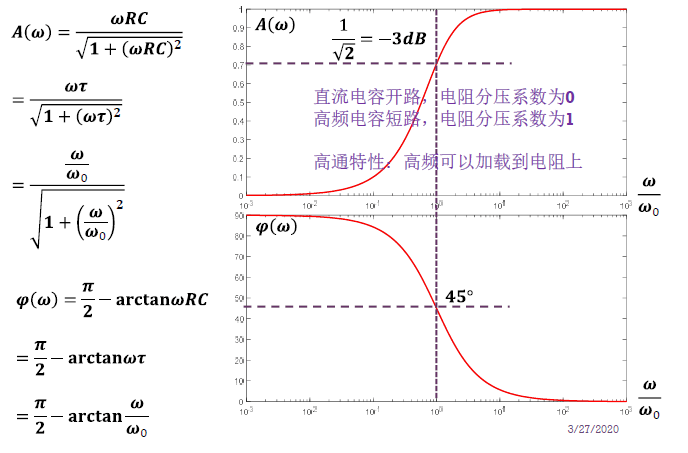
其中 $\omega_0 = \dfrac{1}{\tau} = \dfrac{1}{RC}$。

RC 分压网络：一阶低通/高通滤波器

RL 分压网络：一阶低通/高通滤波器

传递函数的定义

没有信源内阻负载电阻的情况：

采用一般性定义：本征电压增益定义。
$$
H(\mathrm{j} \omega) = \frac{\overset{\cdot}{V}_L(\mathrm{j} \omega)}{\overset{\cdot}{V}_S(\mathrm{j} \omega)} = A_{v0} (\mathrm{j} \omega)
$$
有信源内阻和负载电阻的情况：

可采用一般性定义，也可采用基于功率传输的定义。
$$
H(\mathrm{j} \omega) = 2 \sqrt{\frac{R_S}{R_L}} \frac{\overset{\cdot}{V}_L(\mathrm{j} \omega)}{\overset{\cdot}{V}_S(\mathrm{j} \omega)} \\
|H(\mathrm{j} \omega)|^2 = 4 \frac{R_S}{R_L} \frac{\overset{\cdot}{V}_L(\mathrm{j} \omega)^2}{\overset{\cdot}{V}_S(\mathrm{j} \omega)^2} = \frac{\overset{\cdot}{V}_L(\mathrm{j} \omega) / 2R_L}{\overset{\cdot}{V}_S(\mathrm{j} \omega) / 8R_S} = \frac{P_L(\mathrm{j} \omega)}{P_{S,max}(\mathrm{j} \omega)} = G_T(\mathrm{j} \omega)
$$

电压传递函数的一般性定义

直接写答案：

判断这是一个一阶低通。

得到 $H_0$ 和 $\tau$，根据公式即得：
$$
H(\mathrm{j} \omega) = H_0 \frac{1}{1 + \mathrm{j} \omega \tau}
$$
比如下图：

$$
H_0 = \frac{R_L}{R_S + R_L}, \tau = RC, R = \frac{R_S R_L}{R_S + R_L}
$$
$H_0$ 代表中心频点的传递系数，根据低通高通取 $\omega = 0$ 或 $\infty$。

$\tau = RC$，$R$ 为 $C$ 看到的等效电阻（驱动电容的戴维南内阻）。

基于功率传输的传递函数

$$
H(\mathrm{j} \omega) = H_0 \frac{1}{1 + \mathrm{j} \omega \tau} \\
H_0 = \frac{2\sqrt{R_S R_L}}{R_S + R_L}, \tau = RC, R = \frac{R_S R_L}{R_S + R_L}
$$

分析可得，不同的传递函数定义不会改变通带，只改变 $H_0$。

前者是零频点分压系数，后者的平方为零频点的功率传输系数。

阶跃响应和冲激响应

冲激响应的傅里叶变换为传递函数

传递函数（频域响应）恰好就是冲激响应（时域响应）的傅里叶变换，传递函数和冲激响应是一对傅里叶变换对，两者对 LTI 系统的描述是不同视角的等同描述。

RC 分压——加载冲激激励

单位冲激响应的传递函数

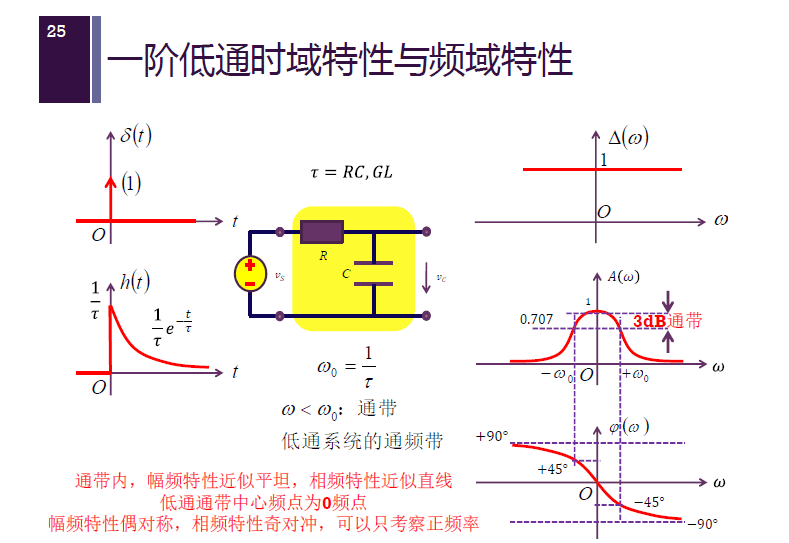
一阶低通/高通时域特性与频域特性

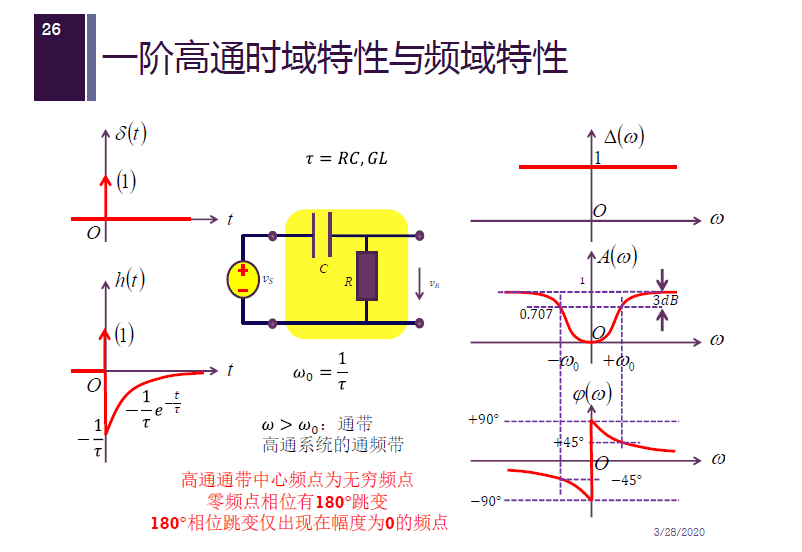
冲激和阶跃

冲激信号及冲激响应的时域波形中， 不容易看清楚哪些是低频变化，哪些是高频变化，而阶跃信号及阶跃响应的时域波形中，却可以很清晰地看出哪里是高频哪里是低频。

冲激响应和阶跃响应

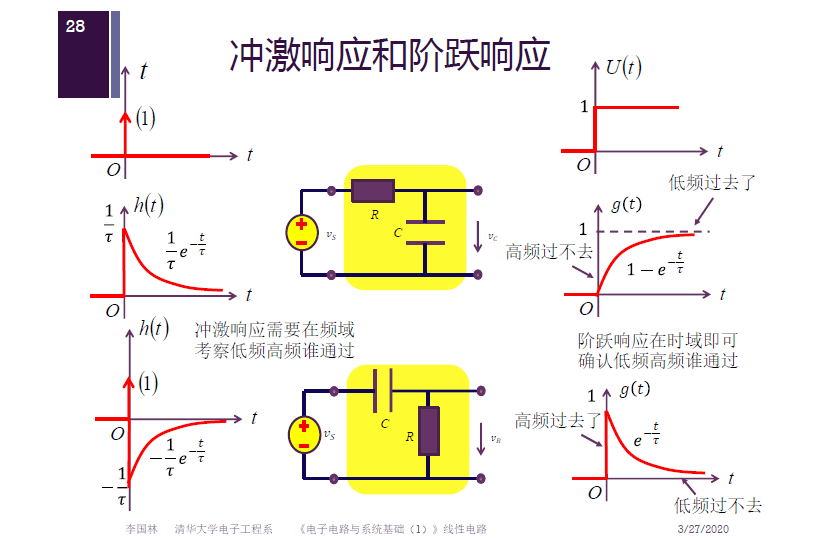
LTI 系统的时域分析与频域分析

频域分析：用相量法求传递函数很简单。

• 频域测量：一个频点一个频点地测量稳态，麻烦耗时；但是测量精度高，因而是当前系统测量的主要方式，如网络分析仪测量的输入阻抗、传递函数等。

时域分析：用时域积分法求解运算过程相当复杂。

• 时域测量：理论上，一个冲激激励，即可获得所有频点的频率响应，因而是相对简单的测量方法：

$$
H(\mathrm{j} \omega) = \int_{-\infty}^\infty h(t) e^{-\mathrm{j} \omega t} \mathrm{d} t
$$

但电路中并不存在冲激信号，电路中的冲激事实上是一种电磁辐射。

在实际时域测量操作时，一般用阶跃激励获得阶跃响应的方式进行测量和分析，原因是阶跃信号容易获得，同时在分析时，通过阶跃响应的时域波形易于理解系统的通带特性。

理论分析时，冲击响应和阶跃响应往往一并考察。

方波信号激励

可以采用三要素法求解，显然 $\tau = RC$，初值 $v_C(0) = 0$，只需要确定稳态响应。

只需要假设方波信号是在 $t = -\infty$ 时加载的，结果就是稳态响应。

电容电压稳态响应分析

直流（冲激、阶跃）激励的稳态响应是直流；正弦激励的稳态响应是正弦波信号；周期信号是稳态响应一定也是同频周期信号。

方波信号的稳态响应如图：

• 周期信号。
• 激励在 $V_{S0}$ 时段内，犹如电容充电，激励在 $0$ 时段，犹如电容放电。

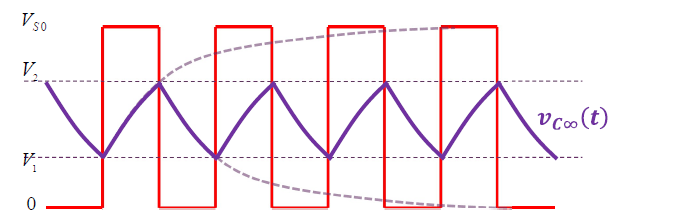
分时段表述

$$
kT_0 \sim (k + 0.5) T_0 : v_{C\infty}(t) = V_{S0} + (V_1 - V_{S0}) e^{-\frac{t - k\tau}{\tau}}, V_{S0} + (V_1 - V_{S0}) e^{-\frac{0.5T_0}{\tau}} = V_2 \\
(k + 0.5) T_0 \sim (k + 1) T_0 : v_{C\infty}(t) = 0 + (V_2 - 0)e^{-\frac{t - (k + 0.5) T_0}{\tau}}, V_2 e^{-\frac{0.5T_0}{\tau} = V_1} \\
V_2 = V_{S0} \frac{1}{1 + e^{-\dfrac{0.5T_0}{\tau}}} \\
V_1 = V_{S0} \frac{e^{-\dfrac{0.5T_0}{\tau}}}{1 + e^{-\dfrac{0.5T_0}{\tau}}} \\
\frac{V_1 + V_2}{2} = 0.5 V_{S0}
$$

代入即得电容电压和电阻电压稳态响应。

波形为：

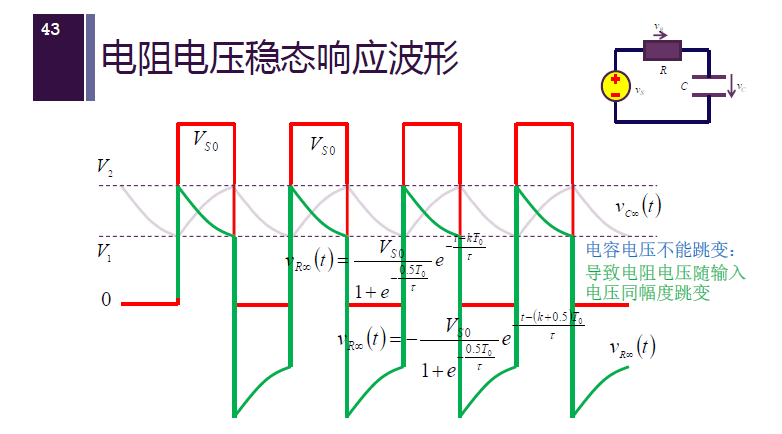
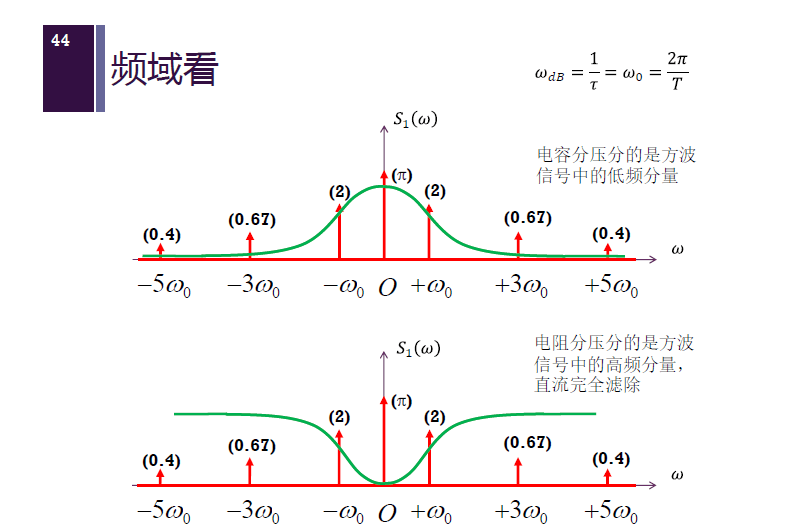
电容电压是输入电压中的低频分量，电容电压平均值为 $0.5 V_{S0}$，取得是直流附近的分量。（灰）

电阻电压是输入电压中的高频分量，电容隔断直流，平均值为 $0$。（绿）

其中从频率看：

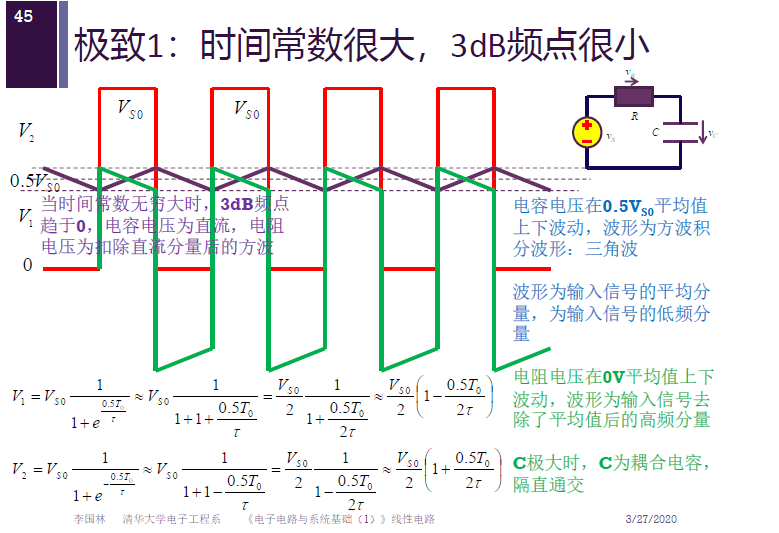
极致 1：时间常数很大，$3 dB$ 频点很小

频域上：

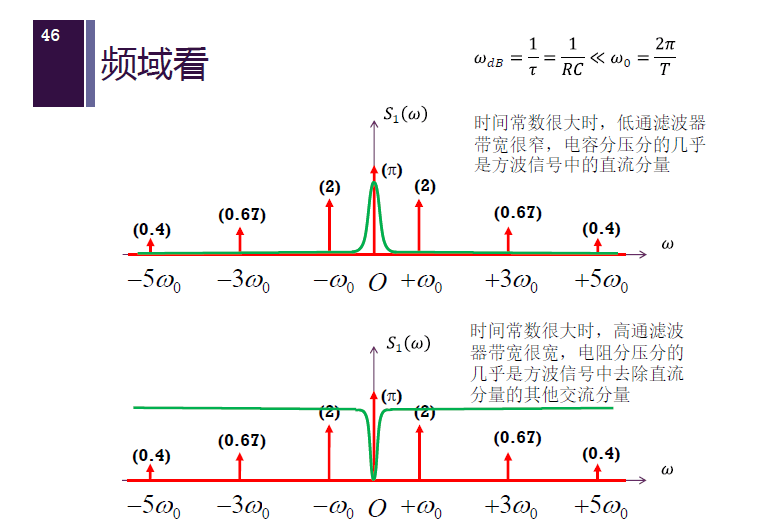
极致 2：时间常数很小，$3 dB$ 频点很大

频域上：

RC 分压：在 $t = 0$ 时刻加载方波激励

$$
v_C(t) = v_{C\infty}(t) + \left(v_C(0^+) - v_{C\infty}(0^+) e^{-\frac{t}{\tau}}\right) \\ = v_{C\infty}(t) - V_{S0} \frac{e^{-\frac{t}{\tau}}}{1 + e^{\frac{0.5T_0}{\tau}}} \\
v_{C\infty}(0^+) = V_{S0} \frac{1}{1 + e^{\frac{0.5T_0}{\tau}}}
$$

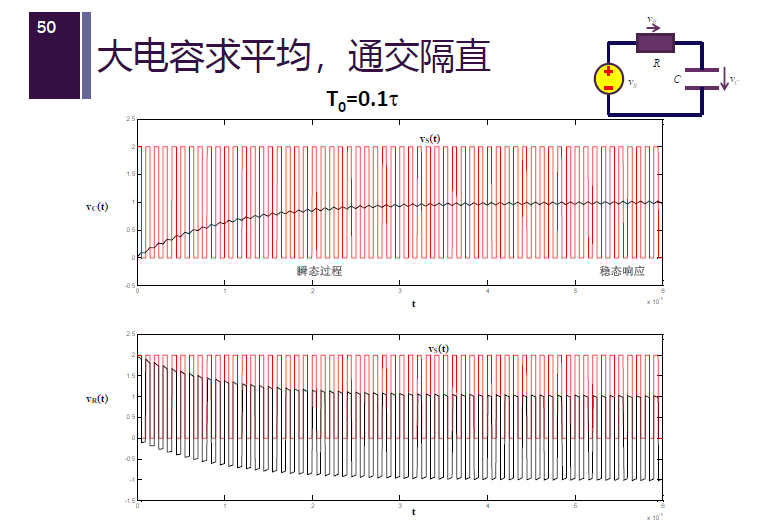
大电容求平均，通交隔直。

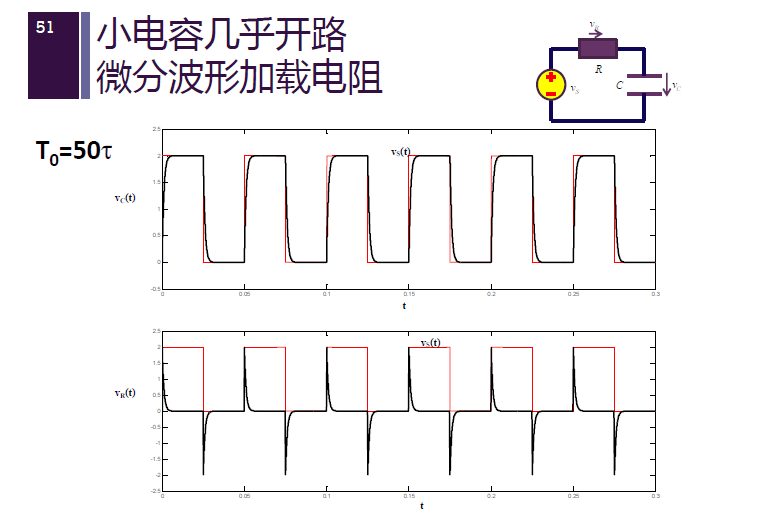
小电容几乎开路，微分波形加载电阻。

 电电 笔记