信号与系统学习笔记（三）

DylanOuO
2021年4月13日

信号与系统学习笔记（三）

卷积

设有两个函数 $f_1(t)$ 和 $f_2(t)$ ,则积分
$$
f(t)=\int_{-\infty}^\infty f_1(\tau)f_2(t-\tau)\mathrm d\tau
$$
称为 $f_1(t)$ 和 $f_2(t)$ 的卷积积分，简称卷积，记为
$$
f(t)=f_1(t)\otimes f_2(t) \qquad or \qquad f(t)=f_1(t)*f_2(t)
$$
利用卷积可以求解系统的零状态响应。

先回顾一下，系统在单位冲激信号 $\delta(t)$ 作用下产生的零状态响应，称为系统的单位冲激响应 $h(t)$ .

假设激励信号为 $e(t)$ ,从第一章的信号分解脉冲分量可以得到，
$$
e(t)=\lim_{\Delta t_1\rightarrow 0}\sum_{t_1=-\infty}^\infty e(t_1)\delta(t-t_1)\Delta t_1\\
r(t)=\lim_{\Delta t_1\rightarrow 0}\sum_{t_1=-\infty}^\infty e(t_1)h(t-t_1)\Delta t_1\\
$$
写为积分形式
$$
r(t)=\int_{-\infty}^\infty e(\tau)h(t-\tau)\mathrm d\tau\\
r_{zs}(t)=e(t)*h(t)
$$
即系统的零状态响应等于激励信号与单位冲激响应的卷积。( LTI )

e.g.

笔记本电脑图床有点问题所以先不传图了，想象一下。

$\text{RL}$ 串联电路，激励信号为电压源 $e(t)$ ,响应为电流 $i(t)$ ,求冲激响应 $h(t)$ ，并求 $e(t)=u(t)-u(t-t_0)$ 时的响应 $i(t)$ .

解

先列方程
$$
Li'(t)+Ri(t)=e(t)\\
$$
$\delta(t)$ 配平得到 $i(0_+)=\dfrac{1}{L}$ ,特征根显然为 $\alpha=-\dfrac{R}{L}$,得到冲激响应
$$
h(t)=\frac{1}{L}e^{-\frac{R}{L}t}u(t)
$$
进行卷积
$$
\begin{align*}
i(t)&=(u(t)-u(t-t_0))*(\frac{1}{L}e^{-\frac{R}{L}t}u(t))\\
&=(u(t)-u(t-t_0))\int_0^t\frac{1}{L}e^{-\frac{R}{L}(t-\tau)}\mathrm d\tau+u(t-t_0)\int_0^{t_0}\frac{1}{L}e^{-\frac{R}{L}(t-\tau)}\mathrm d\tau\\
&=(u(t)-u(t-t_0))\frac{1}{R}(1-e^{-\frac{R}{L}t})+u(t-t_0)\frac{1}{R}(e^{-\frac{R}{L}(t-t_0)}-e^{-\frac{R}{L}t})\\
&=\frac{1}{R}(1-e^{-\frac{R}{L}t})u(t)-\frac{1}{R}(1-e^{-\frac{R}{L}(t-t_0)})u(t-t_0)
\end{align*}
$$
关于积分上下限如果看不出来，可以画图将其中一个信号反褶再平移，观察两信号的重合部分确定积分界限。

卷积的性质

交换律

$$
f_1(t)*f_2(t)=f_2(t)*f_1(t)
$$

证：
$$
f_1(t)*f_2(t)=\int_{-\infty}^\infty f_1(\tau)f_2(t-\tau)\mathrm d\tau\\
=\int_{-\infty}^\infty f_1(t-\lambda)f_2(\lambda)\mathrm d\lambda\\
=f_2(t)*f_1(t)
$$

分配律

$$
f(t)*[h_1(t)+h_2(t)]=f(t)*h_1(t)+f(t)*h_2(t)
$$

相当于系统并联

结合律

$$
f(t)*h_1(t)*h_2(t)=f(t)*[h_1(t)*h_2(t)]
$$

证：
$$
\begin{align*}
f(t)*h_1(t)*h_2(t)=&\int_{-\infty}^\infty[\int_{-\infty}^\infty f(\lambda)h_1(\tau-\lambda)\mathrm d\lambda]h_2(t-\tau)\mathrm d\tau\\
=&\int_{-\infty}^\infty f(\lambda)[\int_{-\infty}^\infty h_1(\tau-\lambda)h_2(t-\tau)\mathrm d\tau]\mathrm d\lambda\\
=&\int_{-\infty}^\infty f(\lambda)[\int_{-\infty}^\infty h_1(\tau)h_2(t-\lambda-\tau)\mathrm d\tau]\mathrm d\lambda\\
=&f(t)*[h_1(t)*h_2(t)]
\end{align*}
$$

微积分性质

$$
g'(t)=f(t)*h'(t)=f'(t)*h(t)
$$

证：
$$
\frac{\mathrm d}{\mathrm dt}[f(t)*h(t)]=\frac{\mathrm d}{\mathrm dt}\int_{-\infty}^\infty f(\tau)h(t-\tau)\mathrm d\tau\\
=\int_{-\infty}^{\infty}f(\tau)\frac{\mathrm dh(t-\tau)}{\mathrm dt}\mathrm d\tau\\
=f(t)*h'(t)
$$
推广
$$
g^{(n-m)}(t)=f^{(n)}(t)*h^{(-m)}(t)
$$
$n$ 为微分 ，$-m$ 为积分。

条件
$$
f(-\infty)=0\\
h(-\infty)=0
$$

与冲激函数卷积

$$
f(t)*\delta(t)=\int_{-\infty}^\infty f(\tau)\delta(t-\tau)\mathrm d\tau\\
=f(t)
$$

推广
$$
f(t)*\delta^{(k)}(t-t_0)=f^{(k)}(t-t_0)
$$

e.g.

$$
e(t)=u(t+\frac{1}{2})-u(t-1)\\
h(t)=\frac{1}{2}t(u(t)-u(t-2))
$$

求卷积

解
$$
e(t)*h(t)=e'(t)*\int_{-\infty}^th(\lambda)\mathrm d\lambda\\
e'(t)=\delta(t+\frac{1}{2})-\delta(t-1)\\
\int_{-\infty}^th(\lambda)\mathrm d\lambda=\int_{-\infty}^t\frac{1}{2}\tau(u(\tau)-u(\tau-2))\mathrm d\tau\\
=\frac{1}{4}t^2u(t)-\frac{1}{4}(t^2-4)u(t-2)\\
=\frac{1}{4}t^2(u(t)-u(t-2))+u(t-2)\\
e'(t)*h^{(-1)}(t)=\frac{1}{4}(t+\frac{1}{2})^2(u(t+\frac{1}{2})-u(t-\frac{3}{2}))+u(t-\frac{3}{2})-\\
\{\frac{1}{4}(t-1)^2(u(t-1)-u(t-3))+u(t-3)\}
$$

算子符号

由于方程式中一些运算符号书写起来不是很方便，所以利用算子符号化简。

算子符号的基本规则

微分和积分用如下表示
$$
p=\frac{\mathrm d}{\mathrm dt}\\
\frac{1}{p}=\int_{-\infty}^t(\cdot)\mathrm d\tau\\
px=\frac{\mathrm d}{\mathrm dt}x\\
p^nx=\frac{\mathrm d^n}{\mathrm dt^n}x\\
\frac{1}{p}x=\int_{-\infty}^tx\mathrm d\tau
$$
比如下面的微分方程
$$
\frac{\mathrm d^2r(t)}{\mathrm dt^2}+5\frac{\mathrm dr(t)}{\mathrm dt}+6r(t)=\frac{\mathrm de(t)}{\mathrm dt}+3e(t)
$$
可以用算子符号写为
$$
p^2r+5pr+6r=pe+3e\\
(p^2+5p+6)r=(p+3)e
$$
注意这是算子方程，表示微分方程，而不是代数方程，有以下的运算规则

• $p$ 多项式可以进行因式分解或展开，如
  $$
  \begin{align*}
  (p^2+5p+6)x&=(p+3)(p+2)x\\
  &=(\frac{\mathrm d}{\mathrm dt}+3)(\frac{\mathrm d}{\mathrm dt}x+2x)\\
  &=\frac{\mathrm d}{\mathrm dt}[\frac{\mathrm d}{\mathrm dt}x+2x]+3[\frac{\mathrm d}{\mathrm dt}x+2x]\\
  &=\frac{\mathrm d^2}{\mathrm dt^2}x+5\frac{\mathrm d}{\mathrm dt}x+6x
  \end{align*}
  $$

• 等式两端的符号 $p$ 不可任意消去

  若
  $$
  \frac{\mathrm dx}{\mathrm dt}=\frac{\mathrm dy}{\mathrm dt}\\
  x=y+C
  $$
  可见
  $$
  px=py\nLeftrightarrow x=y
  $$

• 微分和积分顺序不能倒换
  $$
  p\cdot\frac{1}{p}x=\frac{\mathrm d}{\mathrm dt}\int_{-\infty}^tx\mathrm d\tau=x\\
  \frac{1}{p}\cdot px=\int_{-\infty}^t\frac{\mathrm d}{\mathrm dt}x\mathrm d\tau=x(t)-x(-\infty)\ne x
  $$

用算子符号建立微分方程

对电感
$$
v_L(t)=L\frac{\mathrm d}{\mathrm dt}i(t)=Lpi_L(t)
$$
对电容
$$
v_C(t)=\frac{1}{C}\int_{-\infty}^ti_C(\tau)\mathrm d\tau=\frac{1}{Cp}i_C(t)
$$

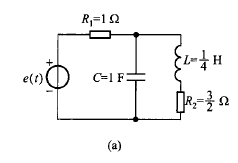
如图所示系统，电路的回路方程为
$$
\begin{cases}
(R_1+\dfrac{1}{Cp})i(t)-\dfrac{1}{Cp}i_L(t)=e(t)\\
-\dfrac{1}{Cp}i(t)+(Lp+R_2+\dfrac{1}{Cp})i_L(t)=0
\end{cases}
$$
求解 $i(t)$ 只需 $Cramer$ 这里就不写了，可以得到 $i$ 和 $e$ 的微分方程。

传输算子

对于高阶的微分方程可以表示为
$$
C_0p^nr(t)+C_1p^{n-1}r(t)+\cdots+C_{n-1}pr(t)+C_nr(t)=E_0p^me(t)+E_1p^{m-1}e(t)+\cdots+E_{m-1}pe(t)+E_me(t)\\
(C_0p^n+C_1p^{n-1}+\cdots+C_{n-1}p+C_n)r(t)=(E_0p^m+E_1p^{m-1}+\cdots+E_{m-1}p+E_m)e(t)
$$
令
$$
\begin{cases}
D(p)=C_0p^n+C_1p^{n-1}+\cdots+C_{n-1}p+C_n\\
N(p)=E_0p^m+E_1p^{m-1}+\cdots+E_{m-1}p+E_m
\end{cases}
$$
则上式可化简为
$$
D(p)[r(t)]=N(p)[e(t)]\\
r(t)=\frac{N(p)}{D(p)}e(t)
$$
其中 $H(p)=\dfrac{N(p)}{D(p)}$ 定义为系统传输算子。

牛刀小试

设 $H(p)$ 是 $LIT$ 系统的传输算子，起始状态为零，试证明
$$
[H(p)\delta(t)]e^{-\alpha t}=H(p+\alpha)\delta(t)
$$

 信号与系统