信号与系统学习笔记（四）

信号与系统学习笔记（四）

开始傅里叶

周期信号傅里叶级数分析

假设有 $n$ 个函数 $g_1(t),g_2(t),\cdots,g_n(t)$ 构成的一个函数集，这些函数在区间 $(t_1,t_2)$ 内满足如下正交特性：

$$\int_{t_1}^{t_2}g_i(t)g_j(t)\mathrm dt=0 \qquad (i\ne j)\\ \int_{t_1}^{t_2}g_i^2(t)\mathrm dt=K_i \qquad 且 \qquad K_i\ne 0$$
则此函数集称为正交函数集。

如果在正交函数集 $\{\varphi_1(t),\varphi_2(t),\cdots,\varphi_n(t)\}$ 之外不存在函数 $\psi(t)(0<\displaystyle{\int_{t_1}^{t_2}\psi^2(t)\mathrm dt<\infty})$ 满足等式

$$\int_{t_1}^{t_2}\psi(t)\varphi_i(t)\mathrm dt=0 \qquad(i=1,2,\cdots,n)$$ 则称该正交函数集为完备正交函数集。若复函数集 $\{\varphi_1(t),\varphi_2(t),\cdots,\varphi_n(t)\}$ 在区间 $(t_1,t_2)$ 满足 $$\int_{t_1}^{t_2}\varphi_i(t)\varphi_j^*(t)\mathrm dt= \begin{cases} 0,&i\ne j\\ K_i\ne 0 &i=j \end{cases}$$ 则称该复函数集为正交函数集。三角函数集 $\{1,\cos(\Omega t),\cos(2\Omega t),\cdots,\cos(m\Omega t),\cdots,\sin(\Omega t),\sin(2\Omega t),\cdots,\sin(n\Omega t),\cdots\}$ 在区间 $(t_0,t_0+T)$ ($T=\dfrac{2\pi}{\Omega})$ 组成完备正交函数集 $$\int_{t_0}^{t_0+T}\cos(m\Omega t)\sin(n\Omega t)\mathrm dt=0\\ \int_{t_0}^{t_0+T}\cos(m\Omega t)\cos(n\Omega t)\mathrm dt= \begin{cases} \dfrac{T}{2},&m=n\ne0\\ 0,&m\ne n \end{cases}\\ \int_{t_0}^{t_0+T}\sin(m\Omega t)\sin(n\Omega t)\mathrm dt= \begin{cases} \dfrac{T}{2},&m=n\ne0\\ 0,&m\ne n \end{cases}\\ $$

三角形式

狄氏条件：

• 周期内间断点个数有限

• 周期内极值数目有限

• 周期内信号绝对可积，即
  

  $$\int_{t_0}^{t_0+T}|f(t)|\mathrm dt$$
  为有限值

周期信号 $f(t)$,周期为 $T_1$ ,基波角频率为 $\omega_1=\dfrac{2\pi}{T_1}$ ，若满足狄氏条件，则可展开成

$$f(t)=a_0+\sum_{n=1}^\infty[a_n\cos(n\omega_1t)+b_n\sin(n\omega_1t)]$$
称为三角形式的傅里叶级数，其系数

直流分量

$$a_0=\frac{1}{T_1}\int_{t_0}^{t_0+T_1}f(t)\mathrm dt$$
余弦幅度
$$a_n=\frac{2}{T_1}\int_{t_0}^{t_0+T_1}f(t)\cos(n\omega_1 t)\mathrm dt$$
正弦幅度
$$b_n=\frac{2}{T_1}\int_{t_0}^{t_0+T_1}f(t)\sin(n\omega_1 t)\mathrm dt$$
e.g.

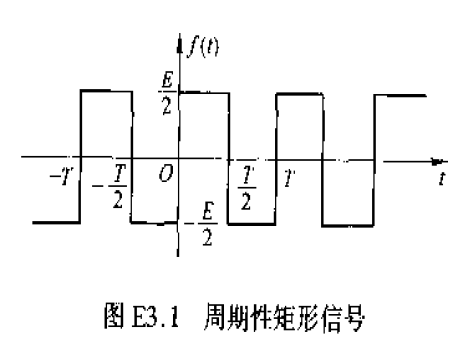
求如图信号的傅里叶级数

解

由于奇对称，所以 $a_0,a_n$ 都为 0

$$b_n=2\cdot\frac{2}{T}\cdot\frac{E}{2}\int_0^{\frac{T}{2}}\sin(n\omega t)\mathrm dt=\frac{E}{n\pi}(1-\cos n\pi)\\ f(t)=\frac{2E}{\pi}\sin(\omega t)+\frac{2E}{3\pi}\sin(3\omega t)+\cdots$$
其他的一些形式

余弦形式

$$f(t)=c_0+\sum_{n=1}^\infty c_n\cos(n\omega_1t+\varphi_n)\\ c_0=a_0,c_n=\sqrt{a_n^2+b_n^2},\varphi_n=\arctan(\frac{-b_n}{a_n}),a_n=c_n\cos\varphi_n,b_n=-c_n\sin\varphi_n$$
正弦形式同理
$$f(t)=d_0+\sum_{n=1}^\infty d_n\sin(n\omega_1t+\varphi_n)\\ d_0=a_0,d_n=\sqrt{a_n^2+b_n^2},\theta_n=\arctan(\frac{b_n}{a_n}),a_n=d_n\sin\theta_n,b_n=d_n\cos\theta_n$$
可以发现频率分量一定是基频 $f_1=\dfrac{1}{T_1}$ 的整数倍，把频率为 $f_1$ 的分量称为基波，频率为 $2f_1,3f_1,\cdots$ 的分量称为二次谐波，三次谐波，$\cdots$ 。

周期信号可分解为直流，基波 $(\omega_1)$ 和各次谐波的线性组合，可以作出幅度频谱图和相位频谱图。

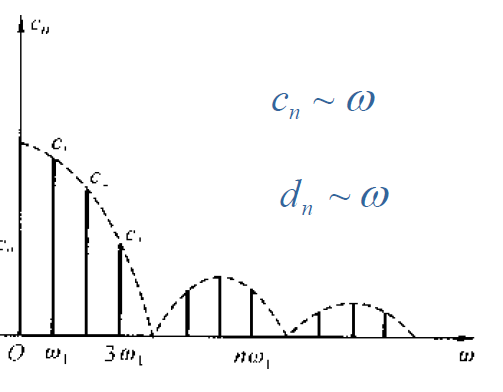
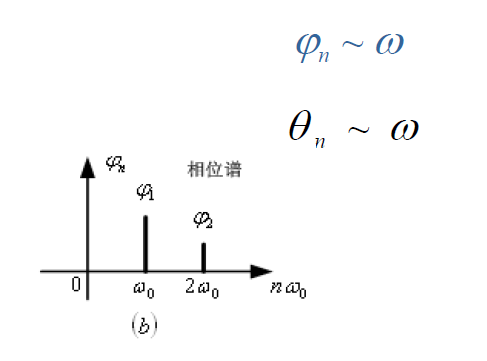
指数形式

复函数集 $\{e^{jn\Omega t}\}$ $(n=0,\pm1,\pm2,\cdots)$ 在区间 $(t_0,t_0+T)$ 内是完备的正交函数集，式中 $T=\dfrac{2\pi}{\Omega}$

$$\int_{t_0}^{t_0+T} e^{jn\Omega t}(e^{jm\Omega t})^*\mathrm dt=\int_{t_0}^{t_0+T} e^{j(n-m)\Omega t}\mathrm dt\\ = \begin{cases} T &n=m\\ 0 &n\ne m \end{cases}$$

$$\cos(n\omega_1t)=\frac{1}{2}(e^{jn\omega_1t}+e^{-jn\omega_1t})\\ \sin(n\omega_1t)=\frac{1}{2j}(e^{jn\omega_1t}-e^{-jn\omega_1t})\\ \begin{cases} a_n=\displaystyle{\frac{2}{T_1}\int_{t_0}^{t_0+T_1}f(t)\cos(n\omega_1 t)\mathrm dt}\\ b_n=\displaystyle\frac{2}{T_1}\int_{t_0}^{t_0+T_1}f(t)\sin(n\omega_1 t)\mathrm dt\\ \end{cases}\\ a_n\cos(n\omega_1t)+b_n\sin(n\omega_1t)=\frac{1}{2}((a_n-jb_n)e^{jn\omega_1t}+(a_n+jb_n)e^{-jn\omega_1t})$$

把 $f(t)$ 写成 $f(t)=a_0+\displaystyle\sum_{n=-\infty}^\infty F_n e^{jn\omega_1t}$ 的形式，则

$$F_n=\frac{1}{2}(a_n-jb_n)$$
代入 $a_n,b_n$
$$F_n=\frac{1}{T_1}\int_{t_0}^{t_0+T_1}f(t)e^{-jn\omega_1t}\mathrm dt$$
有关系
$$F_0=c_0=d_0=a_0\\ F_n=|F_n|e^{j\varphi_n}=\frac{1}{2}(a_n-jb_n)\\ F_{-n}=|F_{-n}|e^{-j\varphi_n}=\frac{1}{2}(a_n+jb_n)\\ |F_n|=|F_{-n}|=\frac{1}{2}c_n=\frac{1}{2}d_n=\frac{1}{2}\sqrt{a_n^2+b_n^2}\\ F_n+F_{-n}=a_n\\ \varphi_n=\arctan\frac{-b_n}{a_n}$$

根据

$$F_n=|F_n|e^{j\varphi_n}$$
可以画出幅度谱 $|F_n| – \omega$ 和相位谱 $\varphi_n – \omega$ .

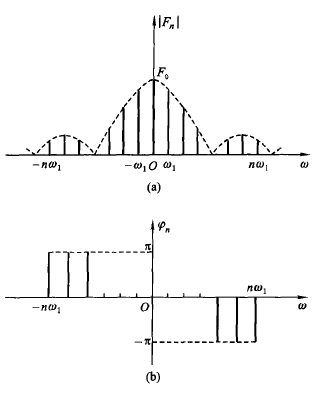
当 $F_n$ 为实数时，可以合画到一张谱上，用正负表示相位。

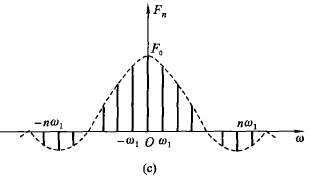
负频率实际上是数学运算的结果，并没有实际物理意义，只有把对应频率的谱线矢量相加才表示该频率幅度。

平均功率

$$P=\overline{f^2(t)}=\frac{1}{T_1}\int_{t_0}^{t_0+T_1}f^2(t)\mathrm dt\\ =\sum_{n=-\infty}^\infty|F_n|^2$$
e.g.

求三角形式中的例题中的那信号的指数傅里叶级数

解

$$F_n=-\frac{E}{2T}\int_{-\frac{T}{2}}^0e^{-jn\frac{2\pi}{T}t}\mathrm dt+\frac{E}{2T}\int_0^{\frac{T}{2}}e^{-jn\frac{2\pi}{T}t}\mathrm dt\\ =\frac{E}{j2n\pi}(1-\frac{e^{jn\pi}+e^{-jn\pi}}{2})=\frac{E}{j2n\pi}(1-\cos(jn\pi))\\ f(t)=\sum_{n=-\infty}^\infty\frac{E}{j2n\pi}(1-\cos(jn\pi))e^{jn\frac{2\pi}{T}t}$$

对称性

1. 偶函数

   信号是偶函数，那么 $f(t)\cos(n\omega_1t)$ 也是偶函数，而 $f(t)\sin(n\omega_1t)$ 是奇函数，
   

   $$a_n=\frac{4}{T_1}\int_0^{\frac{T_1}{2}}f(t)\cos(n\omega_1t)\mathrm dt\\ b_n=0$$
   同时可以得到
   $$2F_n=2a_n\\ \varphi_n=0$$
   只有余弦项

2. 奇函数

   同上， $f(t)\cos(n\omega_1t)$ 是奇函数，而 $f(t)\sin(n\omega_1t)$ 是偶函数
   

   $$a_n=0\\ b_n=\frac{4}{T_1}\int_0^{\frac{T_1}{2}}f(t)\sin(n\omega_1t)\mathrm dt$$
   同时可以得到
   $$2jF_n=b_n\\ \varphi_n=-\frac{\pi}{2}$$
   只有正弦项

3. 奇谐函数

   沿时间轴平移半个周期后相对于 t 轴上下翻转，即
   

   $$f(t)=-f(t\pm\frac{T_1}{2})$$
   

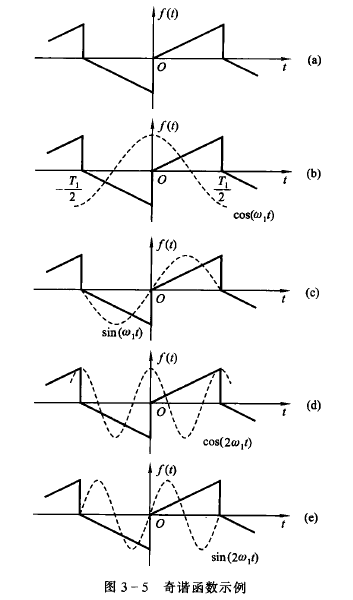
   显然直流分量为 0.

   可以发现图中的 $(b)(c)$ 是可积的，而 $(d)(e)$ 积分为 0，类推可以得到
   

   $$\begin{align*} &a_0=0 \\ &a_n=b_n=0&n为偶数\\ &a_n=\frac{4}{T_1}\int_0^{\frac{T_1}{2}}f(t)\cos(n\omega_1t)\mathrm dt&n为奇数\\ &b_n=\frac{4}{T_1}\int_0^{\frac{T_1}{2}}f(t)\sin(n\omega_1t)\mathrm dt&n为奇数\\ \end{align*}$$
   所以半波对称周期函数的傅里叶级数只含有基波和奇次谐波。偶谐类似我就不再写了。

有限级数和最小方均误差

$$f(t)=a_0+\sum_{n=1}^\infty[a_n\cos(n\omega_1t)+b_n\sin(n\omega_1t)]$$

用前 $2N+1$ 项来逼近

$$S_N(t)=a_0+\sum_{n=1}^N[a_n\cos(n\omega_1t)+b_n\sin(n\omega_1t)]$$
则误差为
$$\varepsilon_N(t)=f(t)-S_N(t)$$
方均误差为
$$E_N=\overline{\varepsilon_N^2(t)}=\frac{1}{T_1}\int_{t_0}^{t_0+T_1}\varepsilon_N^2(t)\mathrm dt\ =\overline{f^2(t)}-[a_0^2+\frac{1}{2}\sum_{n=1}^N(a_n^2+b_n^2)]$$

接下来是一些典型信号。

典型周期信号的傅里叶级数

周期矩形脉冲

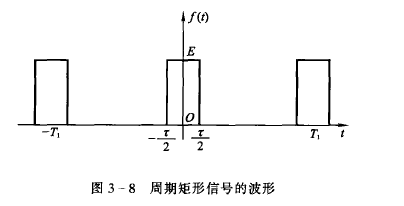
周期内

$$f(t)=E[u(t+\frac{\tau}{2})-u(t-\frac{\tau}{2})]$$
显然
$$a_0=E\tau/T_1$$
计算
$$a_n=\frac{4E}{T_1}\int_0^\frac{\tau}{2}\cos(n\frac{2\pi}{T_1}t)\mathrm dt=\frac{2E}{n\pi}\sin\frac{n\pi\tau}{T_1}$$
引入抽样函数
$$Sa(t)=\frac{\sin t}{t}$$
则
$$a_n=\frac{2E\tau}{T_1}Sa(\frac{n\pi\tau}{T_1})$$
同时由于是偶函数，所以
$$b_n=0$$
三角级数为
$$f(t)=\frac{E\tau}{T_1}+\frac{2E\tau}{T_1}\sum_{n=1}^\infty Sa(\frac{n\pi\tau}{T_1})\cos(n\omega_1t)$$
指数形式
$$F_n=\frac{E}{T_1}\int_{-\frac{\tau}{2}}^{\frac{\tau}{2}}e^{-jn\omega_1t}\mathrm dt=\frac{E}{jn\omega_1T_1}\cdot\sin(n\omega_1\tau/2)\cdot2j=\frac{E\tau}{T_1}Sa(\frac{n\omega_1\tau}{2})\ f(t)=\frac{E\tau}{T_1}\sum_{n=1}^\infty Sa(\frac{n\omega_1\tau}{2})e^{jn\omega_1t}$$

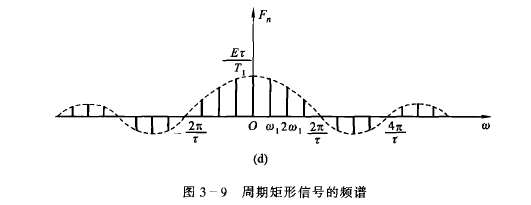
– 可以发现频谱是离散的，而且 $T_1$ 越大， $\omega_1$ 越小，谱线越密集

• 包络线为抽样函数

• 能量主要集中在第一个零点以内，通常把 $\omega=0 \sim\dfrac{2\pi}{\tau}$ 称为频带宽度，记作
  

  $$B_\omega=\frac{2\pi}{\tau}\\ B_f=\frac{1}{\tau}$$

功率

$$P=F_0+2\sum_{n=1}^\infty|F_n|^2\\ P_{5n}=F_0+2\sum_{n=1}^4|F_n|^2=0.181E^2\approx P=0.2E^2$$
对于一般周期信号，将幅度下降为 $\dfrac{1}{10}|F_n|_{max}$ 的区间定义为频带宽度

傅里叶变换

若 $T_1\rightarrow \infty$ ,则 $\omega_1\rightarrow 0$ ,周期信号拓展到非周期信号，离散频谱变为连续谱，谱系数 $F_n$ 无限小，引入频谱密度函数。

$$F(\omega)=\lim_{T_1\rightarrow\infty}T_1F(n\omega_1)=\lim_{T_1\rightarrow\infty}\int_{-\frac{T_1}{2}}^\frac{T_1}{2}f(t)e^{-jn\omega_1t}\mathrm dt=\int_{-\infty}^\infty f(t)e^{-j\omega t}\mathrm dt=\mathscr F[f(t)]$$
由 $f(t)$ 求 $F(\omega)$ 称为傅里叶变换。
$$F(\omega)=|F(\omega)|e^{j\varphi(\omega)}\\ $$
同样有幅度频谱（习惯上称为）和相位频谱。
$$f(t)=\lim_{T_1\rightarrow\infty}\sum_{n=-\infty}^\infty F(n\omega_1)e^{jn\omega_1t}=\lim_{T_1\rightarrow\infty}\sum_{n=-\infty}^\infty \frac{F(\omega)}{2\pi}\cdot \omega_1\cdot e^{jn\omega_1t}=\frac{1}{2\pi}\int_{-\infty}^\infty F(\omega)e^{j\omega t}\mathrm dt=\mathscr F^{-1}[F(\omega)]$$
由 $F(\omega)$ 求 $f(t)$ 称为傅里叶逆变换。$f(t)\leftrightarrow F(\omega)$ 为傅里叶变换对。
$$f(t)=f_e(t)(偶分量)+f_o(t)(奇分量)$$

$$F(\omega)=\int_{-\infty}^\infty f(t)e^{-j\omega t}\mathrm dt\\ =2\int_0^\infty f_e(t)\cos(\omega t)\mathrm dt-2j\int_0^\infty f_o(t)\sin(\omega t)\mathrm dt$$

$$R(\omega)=2\int_0^\infty f_e(t)\cos(\omega t)\mathrm dt\\ X(\omega)=-2\int_0^\infty f_o(t)\sin(\omega t)\mathrm dt\\ |F(\omega)|=\sqrt{R^2(\omega)+X^2(\omega)}\\ \varphi(\omega)=\arctan\frac{X(\omega)}{R(\omega)}$$

物理意义

把 $f(t)$ 改写为三角函数形式，

$$f(t)=\frac{1}{2\pi}\int_{-\infty}^\infty |F(\omega)|e^{j\varphi(\omega)}\cdot e^{j\omega t}\ \mathrm d\omega\\ =\frac{1}{2\pi}\int_{-\infty}^\infty|F(\omega)|\cos(\omega t+\varphi(\omega))\mathrm d\omega+\frac{j}{2\pi}\int_{-\infty}^\infty|F(\omega)|\sin(\omega t+\varphi(\omega))\mathrm d\omega$$

显然，若 $f(t)$ 为实函数，则

$$f(t)=\frac{1}{\pi}\int_0^\infty|F(\omega)|\cos[\omega t +\varphi(\omega)]\mathrm d\omega$$
信号可以分解为许多不同频率的正余弦分量，任一能量有限的信号在各频率点的分量幅度 $\dfrac{|F(\omega)|\mathrm d\omega}{\pi}$ 无限小，所以不再用幅度表示频谱而用密度函数。

变换条件 $f(t)$ 无限区间内绝对可积

e.g.

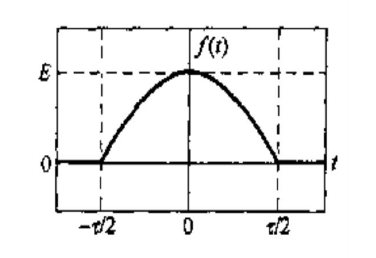
如图为半波余弦脉冲，求傅里叶变换并画出频谱。

解

$$f(t)= \begin{cases} E\cos(\dfrac{\pi}{\tau}t)&|t|<\dfrac{\tau}{2}\\ 0 &其他 \end{cases}\\ F(\omega)=2\int_0^{\frac{\tau}{2}}E\cos(\frac{\pi}{\tau}t)\cos(\omega t)\mathrm dt\\ =E\{\int_0^\frac{\tau}{2}\cos[(\frac{\pi}{\tau}+\omega)t]\mathrm dt+\int_0^\frac{\tau}{2}\cos[(\frac{\pi}{\tau}-\omega)t]\mathrm dt\}\\ =E[\frac{\sin(\frac{\pi}{2}+\frac{\tau}{2}\omega)}{\frac{\pi}{\tau}+\omega}+\frac{\sin(\frac{\pi}{2}-\frac{\tau}{2}\omega)}{\frac{\pi}{\tau}-\omega}]\\ =\frac{E}{(\frac{\pi}{\tau})^2-\omega^2}[(\frac{\pi}{\tau}-\omega)\cos(\frac{\tau}{2}\omega)+(\frac{\pi}{\tau}+\omega)\cos(\frac{\tau}{2}\omega)]\\ =\frac{2E\pi}{\tau[(\frac{\pi}{\tau})^2-\omega^2]}\cos(\frac{\tau\omega}{2})$$ 频谱如图

 信号与系统