
The Physics of Information Lecture Note 2
Contents
Lecture 2
Maxwell-Boltzmann distribution

Suppose a system has $n$ energy levels. Suppose that there are $N_i$ particles at the energy level $E_i$ and the total particle number is fixed, that is, $N=\sum_{i=1}^n N_i$. What determines the distribution of $N_i$ based on the assumption that the equilibrium state corresponds to the state with maximum accessible states?
Consider distinguishable particles, how many configuration do we have?

The total configuration is $\frac{N!}{N_1!N_2!\cdots N_n!}$ (we don't care about the sequence of particles in each level.) If there exist $g_i$ degenerate(简并的) levels in each level $E_i$, we need to further consider the configuration in these sublevels. Degenerate states are different states with the same energy. How many configurations do we have when we put $N_i$ different particles into the $g_i$ container?
For each particle, there is $g_i$ configurations and thus total we have $g_i^{N_i}$ configurations. For example, let $g_i=2,N_i=3$,

total $2^3=8$.
To sum up, we have totally
$$
Q(N_1,N_2,\dots,N_n)=\frac{N!}{\Pi_{i=1}^n N_i!}\cdot\Pi_{i=1}^n g_i^{N_i}
$$
configurations where $N=\sum_i N_i$.
We also have 2 physical constraints :
- $\sum_{i=1}^n N_i=N_0$ , particle number is conserved;
- $\sum_{i=1}^nN_iE_i=U_0$ , the energy is conserved.
Introduce the Lagrange multiplier $\alpha$ and $\beta$ so that
$$
\frac{\partial}{\partial N_i}\log Q+\alpha \frac{\partial N}{\partial N_i}-\beta \frac{\partial U}{\partial N_i}=0.
$$
Here, $\log Q =\log N!+\sum_{i=1}^nN_i\log g_i-\sum_{i=1}^n\log N_i!$ .
For large number $ X $, Stirling's approximation
$$
\log X!\approx X\log X -X.
$$
Thus,
$$
\begin{align}
\log Q&\approx N\log N-N+\sum_{i=1}^nN_i\log g_i-\sum_{i=1}^nN_i\log N_i+\sum_{i=1}^nN_i \\ &=N\log N+\sum_{i=1}^nN_i\log g_i-\sum_{i=1}^nN_i\log N_i.
\end{align}
$$
The above derivative equation becomes
$$
\log N+\log g_i-\log N_i+\alpha-\beta E_i=0
$$
leading to
$$
\log \frac{N_i}{g_iN}=\alpha-\beta E_i,
$$
so that
$$
p_i=\frac{N_i}{g_iN}=\mathrm{e}^{\alpha-\beta E_i}.
$$
In this way, we actually consider the giant canonical ensemble where the total particle number can fluctuate. While the giant canonical ensemble is equivalent to the canonical ensemble, for a large particle number, we may consider the latter one so that there are $n-1$ independent variables $N_1,N_2,\dots,N_{n-1}$. We only need one physical constraint
$$
\frac{\partial}{\partial N_i}\log Q-\beta\frac{\partial U}{\partial N_i}=0,i=1,2,\dots,n-1
$$
where
$$
\log Q=N\log N +\sum_{i=1}^{n-1}N_i\log g_i +N_n\log g_n-\sum_{i=1}^{n-1}N_i\log N_i -N_n\log N_n,\\
N_n=N-\sum_{i=1}^{n-1}N_i,U=\sum_{i=1}^{n-1}E_iN_i+E_nN_n.
$$
$$
\log g_i-\log g_n-\log N_i+\log N_n-\beta(E_i-E_n)=0\\
\Rightarrow \log\left(\frac{N_i}{g_i}\cdot\frac{g_n}{N_n}\right)=-\beta(E_i-E_n)\\
\frac{N_i}{g_i}=\frac{N_n}{g_n}\cdot\mathrm{e}^{-\beta(E_i-E_n)},
$$
which reduces to
$$
\frac{N_i/g_i}{N_n/g_n}=\frac{\mathrm{e}^{-\beta E_i}}{\mathrm{e}^{-\beta E_n}}.
$$
This implies the probability at energy $E_i$ is
$$
p_i=\mathrm{e}^{-\beta E_i}/z
$$
(probability that a particle occupies a state) where $z$ is called the partition function acting as a normalization factor, $z=\sum_{i}\mathrm{e}^{-\beta E_i}$ where $\beta=1/k_BT$. ($\sum_ii$ denotes all the states including degenerate states)
Example. The distribution function of an ideal gas without external force. Since $E=\frac{1}{2}mv^2$, we have
$$
p(v)=\mathrm{e}^{-\frac{mv^2}{2k_BT}}/z.
$$
$v$ takes continuous values, $p(v)$ should be the probability density s.t. $p(v)dv_xdv_ydv_z$ describes the probability that a particle has velocity $[v_x,v_x+dv_x]$, $[v_y,v_y+dv_y]$ ,$[v_z,v_z+dv_z]$.
$$
\begin{align}
z&=\iiint_{-\infty}^{\infty}dv_xdv_ydv_ze^{-\frac{mv^2}{2k_BT}}\\
&=\left(2\int_0^\infty e^{-\frac{mv^2}{2k_BT}}dv\right)^3\\
&=\left(\frac{2\pi k_BT}{m}\right)^{\frac{3}{2}}\text{by Gaussian integral.}
\end{align}
$$
- If the system is in thermal contact with a heat bath, the temperature is the same as that of the bath and the internal energy of the system is determined by the temperature.
- If the system is isolated, the temperature is determined by the internal energy of the system. If we consider the infinite temperature case, i.e. $\beta\to 0$, the probability at all $E_i$ is the same.
If we regard this system as an isolated system, you may think besides the maximum configurations, there also exist other configurations such as $B$ with the same energy. Based on Boltzmann hypothesis, the probability for the $B$ configuration is the same as one of the maximum configurations. For example, suppose the configuration with $N_1=4,N_2=3,N_3=2,N_4=1$ has the maximum accessible states. But it is possible that $N_1=5,N_2=2,N_3=1,N_4=2$ has the same energy as the maximum configuration. Why don't we include these states as a candidate for a system?
The reason is in the thermodynamic limit, the probability at these states are very low.

$$
\log Q(N_1+\Delta N_1,\dots,N_n+\Delta N_n)=\log Q(N_1,\dots,N_n)+\frac{1}{2}\sum_{ij}\partial_{N_i}\partial_{N_j}\log Q(N)\Delta N_i\Delta N_j
$$
*泰勒展开,一阶项为0(因为是极大值),三阶以上的忽略
$$
\Rightarrow \log \frac{Q(N_1+\Delta N_1,\dots,N_n+\Delta N_n)}{Q(N_1,\dots,N_n)}=-\frac{1}{2}\sum_{ij}\delta_{ij}\frac{1}{N_i}\Delta N_i\Delta N_j=-\frac{1}{2}\sum_i\frac{(\Delta N_i)^2}{N_i}=-\frac{1}{2}\sum_i \left(\frac{\Delta N_i}{N_i}\right)^2N_i.
$$
*$\log Q$对$N_i,N_j$求偏导时,$N$当成函数,得到$(1/N-\delta_{ij}/N_i)$;由于$\sum_i \Delta N_i \approx 0$,对某个特定的$i,\sum_j 1/N \Delta N_i \Delta N_j \approx 0$,导致最后化简结果看上去$N$就像是一个常数.
Suppose $\frac{\Delta N_i}{N_i}\sim 10^{-5},N\sim 10^{23}$, we have
$$
\frac{Q(N_1+\Delta N_1,\dots,N_n+\Delta N_n)}{Q(N_1,\dots,N_n)}=e^{-\frac{1}{2}\times 10^{-10}N}\sim e^{-10^{13}}.
$$
Entropy
$$
F=-k_BT\log zN
$$
Since $z=\sum_i e^{-\beta E_i}=e^{-E_i/k_BT}/p_i$ , we have
$$
\begin{align}
F&=-k_BT\log(e^{-E_i/k_BT}/p_i)N=(E_i+k_BT\log p_i)N\\
&=\sum_i p_i(E_i+k_BT\log p_i)N
\end{align}
$$
since $\sum_i p_i=1$. The entropy
$$
S=\frac{U-F}{T}=-N\sum_i k_Bp_i\log p_i,
$$
thus Boltzmann entropy
$$
S=\frac{S'}{N}=-\sum_i k_Bp_i\log p_i
$$
denoting the entropy per particle. Since $p_i=\frac{N_i}{Ng_i}$, we have
$$
\begin{align}
S'&=-Nk_B\sum_i'\frac{N_i}{N}\log N_i/Ng_i\text{ where $\sum_i'$ denotes the sum counting the degenerate energy levels once}\\
&=-k_B\sum_i'(N_i\log N_i-N_i\log N-N_i\log g_i)\\
&=k_BN\log N-k_BN-k_B\sum_i'(N_i\log N_i-N_i-\log g_i^{N_i})\\
&\approx k_B\log N!-k_B\sum_i'(\log N_i!-\log g_i^{N_i})\\
&=k_B\log \frac{N!}{N_1!N_2!\cdots N_n!}\Pi_i g_i^{N_i}=k_B\log Q.
\end{align}
$$
Derive the ideal gas form from Maxwell velocity distribution. Since we also need to consider the spatial freedom, we require
$$
z=V\left(\frac{2\pi k_BT}{m}\right)^{3/2}
$$
so that
$$
\iiint dxdydz\iiint dv_xdv_ydv_z e^{-\frac{mv^2}{2k_BT}}/z=1.
$$
For an isothermal process,
$$
-\Delta F=+nRT\log V_f/V_i=+\Delta W.
$$
Thus
$$
F=-nRT\log V\left(\frac{2\pi k_BT}{m}\right)^{3/2}.
$$
Since
$$
dF=-SdT-pdV,
$$
we have
$$
p=-\left(\frac{\partial F}{\partial V}\right)_T=nRT\cdot \frac{1}{V}\Rightarrow pV=nRT,\\
S=-\left(\frac{\partial F}{\partial T}\right)_V=nR\log V\left(\frac{2\pi k_BT}{m}\right)^{3/2}+\frac{3nR}{2}.
$$
- The degeneracy: $\epsilon=\frac{1}{2}m(v_x^2+v_y^2+v_z^2).$

The Landauer principle (proposed in 1961)
The erasure of data in a system necessarily involves producing heat and thereby increasing the entropy.
Let's consider a vessel(容器) divided into 2 half parts. A bit of information is stored in this vessel based on whether a molecule is located at the left or the right part.
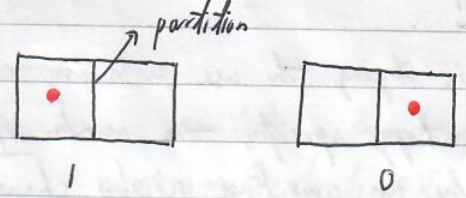
To erase the stored information, we need to move the molecule to a state without carrying any information (called a standard state). For example,

We note that this erasure process is many-to-one mapping, and thus not reversible.
Let's see a procedure to erase the stored information. Before that, we note that we are unaware of the stored information before the process.
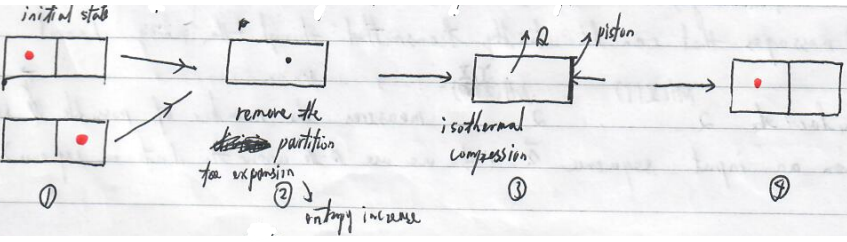
(piston : 活塞)
It is evident that during the isothermal compression, the entropy of the system decreases and heat is generated, flowing to the environment.
$$
Q=\int \bar{d}W=\int pdV=k_BT\int _V^{V/2} \frac{dV}{V}=-k_BT\ln2.
$$
The entropy decrease for the system is $k_B\ln2$.
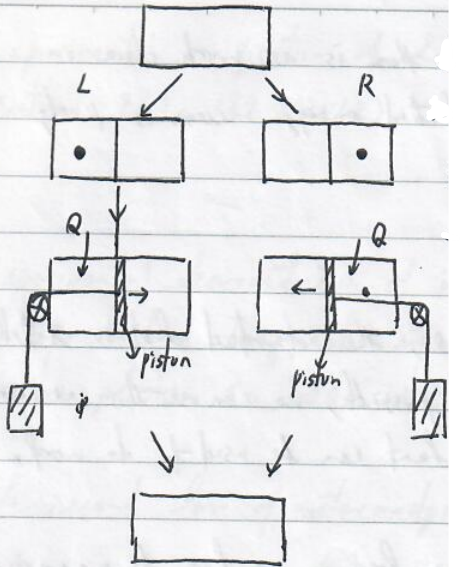
Maxwell's demon
a. temperature demon
Initially in thermal equilibrium with temperature $T$, average velocity <$v$>.
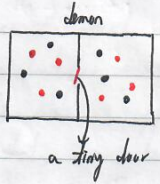
Particles in the left part approaching the door with velocity $>$ <$v$> , open the door; particles in the right part approaching the door with velocity $<$ <$v$> , open the door.

It looks that the system "naturally" forms an ordered phase with hot and cold particles located at the right and left sides.

(insulating : 绝热)
Suppose $T_1
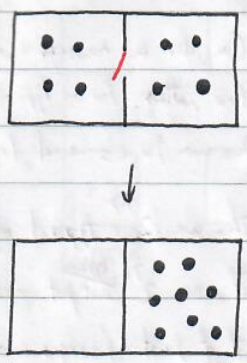
If there is a particle approaching the door in the left side, open the door. All particles are located in the right side box, leading to the increase of the entropy.
Is it possible? What is missing?
We miss the effects of the demon. If we were the demon, we need to recognize whether a particle moves fast or slowly, whether a particle at the left side is approaching. That means we need to measure the state of the particle. Besides that, we also know the state of a particle. In fact, it has been shown that measurement can be reversible and does not necessarily produce any entropy. However, the demon's memory changes.
Szilard's machine ("a perpetual motion machine")
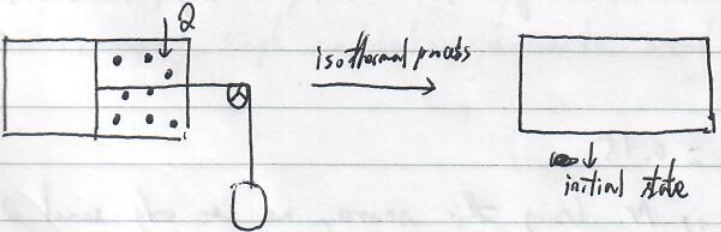
All absorbed heat is used to do work. However,the demon has memorized the positions of all these molecules. To remove these memories requires producing the heat $Q=Nk_BT\ln2$ and entropy increases by $Nk_B\ln2$.
Initially, Maxwell's demon does not know the position of the molecule and he/she knows that he/she does not know. After measurement, the demon stores the information in the memory. Isothermal expansion doing work $W=Q$.
For the system, the final state has the same temperature , pressure, volume with the initial state and thus returns to the original state. We are also happy to see that during this cyclic process, all absorbed heat is used to do work, clearly violating the second law of thermodynamics. However, we neglect the memory state of the demon. To complete a cycle, we also require to return the memory to the original state, that is, we need to erase the stored information. Based on the Landauer principle, this requires to generate heat $k_BT\ln2$.
We note that for a single molecule experiment, we can consider an ensemble of the system, many single molecule experiments, and thus the statistics make sense.



No Comments