The Physics of Information Lecture Note 3

The Physics of Information Lecture Note 3

Lecture 3

Information theory

• data compression (lossless transmission) : What is the best encoding scheme?
• Noisy channel
  • How many auxiliary bits do we need to send besides the original data?
  • How many messages can be reliably transmitted through a noisy channel?

Shannon entropy

Information is used to characterize how surprised you are when you learn something. Mathematically, Shannon defined a quantity called self-information. Suppose we have an event $A$, which is a set of outcomes of some random experiment. If $P(A)$ is the probability that the event $A$ will occur, then self-information associated with $A$ is given by

$$i(A)=-\log_f P(A).$$
Intuitively, it makes sense as a highly probable event gives a low information.

If we have a set of independent events $A_i$, which are sets of outcomes of some experiment, $S=\{A_1,A_2,\dots,A_n\}$, when the average information associated with the random experiment is given by

$$H=-\sum_i P(A_i)\log_f P(A_i)$$
which is exactly the Gibb’s entropy.

Application in data compression

Shannon showed that if the experiment is a source that puts out symbols $A_i$ from a set $A$, then the entropy is a measure of the average number of binary symbols needed to code the output of the source. The best that a lossless compression scheme can do is to encode the output of a source with an average number of bits equal to the entropy of the source.

Source : $\mathbf{X}=\{x_1,x_2,\dots,x_l\}$ with $\{P(x_1),P(x_2),\dots,P(x_l)\}$

Suppose the messages has $N$ letters a piece.

typical message : a message consisting of $NP(x_1)$ number of $x_1$, $NP(x_2)$ number of $x_2$, $\dots$ , $NP(x_l)$ number of $x_l$.

Question : How many typical messages do we have?

$$N_t=\frac{N!}{(NP(x_1))!(NP(x_2))!\dots(NP(x_l))!}\\ \log_2 N_t=\log_2N!-\sum_{i=1}^l \log(NP(x_i))!$$
Using $\log_2N!\approx N\log_2N-N\log_2e$,
$$\begin{align} \log_2N_t&=N\log_2N-N\log_2e-\sum_i(Np_i\log Np_i-Np_i\log_2e)\\ &=-N\sum_iP(x_i)\log_2 P(x_i)=NH. \end{align}$$
Thus,
$$N_t=2^{NH}.$$
It means we can use $NH$ bits in total to encode all these messages, instead of using $N\log_2 l$.

$H=-\sum_i P(x_i)\log_2P(x_i)\longrightarrow$ Shannon entropy

Example : $\{1,2,3,4\}$ with probability $\frac{1}{4}$.

$H=-\sum_i \frac{1}{4} \log_2 \frac{1}{4}=2$.

$$\begin{cases} x_1x_1x_2\dots x_l &1\\ x_1x_2x_1\dots x_{l-1} &2\\ \vdots &\vdots\\ x_2x_3x_1\dots x_1 &2^{NH}\rightarrow\text{NH: number of bits required to store messages, H: average number of bits required to store a letter} \end{cases}$$
Example1 : Let $A=\{a_1,a_2,\dots,a_5\}$ with $P(a_1)=P(a_3)=0.2$, $P(a_2)=0.4,P(a_4)=P(a_5)=0.1$. Use this source to generate messages.

$H=\sum_{i=1}^5 P(a_i)\log_2P(a_i)=2.122$,

Huffman coding :

	codeword
$a_2$	1
$a_1$	01
$a_3$	000
$a_4$	0010
$a_5$	0011

The average bits per symbol using the Huffman coding is

$$0.4+2\times 0.2+3\times 0.2+4\times 0.1+4\times 0.1=2.2​$$
which is larger than $2.122$ by $0.078$.

Example 2 : Consider the following sequence 1 2 3 2 3 4 5 4 5 6 7 8 9 8 9 10. How can we code this sequence?

Simply, we can code each letter by four binary symbols, e.g. 10 = 1010, 2 = 0010. To code this sequence, we require 4 binary symbols per letter (symbol).

Suppose that each number in the sequence occurs independently and the probability is that each number happens is reflected accurately in the sequence. Then $A={1,2,3,4,5,6,7,8,9,10}$ and the associated probabilities are $P(1)=P(6)=P(7)=P(10)=\frac{1}{16}, P(2)=P(3)=P(4)=P(5)=P(8)+P(9)=\frac{2}{16}$. The entropy is calculated as $H=-\sum_{i=1}^{10} P(i)\log_2 P(i)=3.25$.

That means that the best scheme we could find for coding this sequence could only code it at $3.25$ per symbol, which is smaller than $4$ per symbol.

But this sequence has structures. The difference between two neighboring numbers is 1 1 1 -1 1 1 1 -1 1 1 1 1 1 -1 1 1(the first 1 is the initial one since we also need to code this one). In this case, $P(1)=\frac{13}{16},P(-1)=\frac{3}{16},H=0.7$, which is much smaller than the previous one.

This example indicates that it’s not possible to know the entropy of a physical source that generates a sequence unless we are quite clear about the structure of the sequence.

Noisy channels

We may regard $X$ and $Y$ as sets of letters. If the channel is noiseless, the map from $X$ to $Y$ is one-to-one, that is, the outcome of a letter $y$ corresponds to an input of the same letter $y$. However, a channel usually contains noises, which modifies the outcome. How many auxiliary bits do we need to send besides the original data?

Conditional probability $P(y_i \mid x_i)$ : given that input $x_i$ is prepared, the probability that output $y_i$ will be produced.

Noiseless channel : $P(x_j\mid x_i)=\delta_{ij}$

Joint probability $P(x_i\land y_i)$ : the probability that the input is $x_i$ and output is $y_j$.

$P(x_i\land y_j)=P(x_i)P(y_j\mid x_i)=P(y_j)P(x_i\mid y_j).$

$2^{NH(X)}$ : the number of typical distinct input messages

$2^{NH(Y)}$ : the number of typical distinct output messages

Joint entropy (uncertainty) : $H(X\land Y)\equiv-\sum_{ij} P(x_i\land y_j)\log_2P(x_i\land y_j)$

• $H(X\land Y)\ge H(X)$
• Consider the noiseless channel, $P(x_i\land y_j)=\delta_{ij}P(x_i),H(X\land Y)=H(X)$.

Conditional entropy : $H(X\mid Y)\equiv\sum_jP(y_j)\left[-\sum_i P(x_i\mid y_j)\log_2 P(x_i\mid y_j)\right]$

The latter part is the uncertainty for the input for a given output $y_i$. Thus for all $y_j$, $H(X\mid Y)$ gives us the average uncertainty for the input given the outputs.

Noiseless channel : $P(x_i\mid y_j)=\delta_{ij},H(X\land Y)=H(X)=H(Y),H(X\mid Y)=0.$

Completely noisy channel : input and output letters are independent (do not have any correlation)

$P(x_i\mid y_j)=P(x_i),H(X\mid Y)=-\sum_i P(x_i)\log_2 P(x_i)=H(X).$

These two limits tells us

$$H(X\mid Y)\le H(X).$$
The uncertainty of $X$ is never increased by knowledge of $Y$. It will be decreased unless $Y$ and $X$ are independent events, in which case it is not changed.
$$H(X\land Y)=H(X)+H(Y\mid X)=H(Y)+H(X\mid Y)$$
Proof :
$$\begin{align} LHS&=-\sum_{ij}P(x_i\land y_j)\log_2P(x_i\land y_j)\\ &=-\sum_{ij}P(x_i\mid y_j)P(y_j)\left(\log_2P(x_i\mid y_j)+\log_2P(y_j)\right)\\ &=H(X\mid Y)+H(Y) \end{align}$$

Each sequence of pairs of $X,Y$ values represents a map from $X$ to $Y$. Thus $\frac{2^{NH(X\land Y)}}{2^{NH(Y)}}$ represents the average number of distinct sequence of $X$ for a given output. In other words, this number measures the number of possible input sequences that could have given rise to the observed output.

$$\frac{2^{NH(X\land Y)}}{2^{NH(Y)}}=2^{NH(X\mid Y)}$$

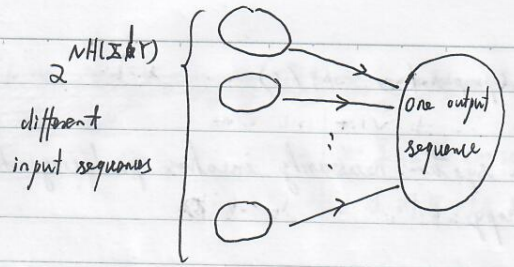
When the channel is noiseless, $H(X\mid Y)=0$ and $2^{NH(X\mid Y)}=1$, suggesting the one-to-one correspondence.

Shannon points out that if one is trying to use a noisy channel to send a message, then the conditional entropy specifies the number of bits per letter that would need to be sent by an auxiliary noiseless channel in order to connect all the errors that have crept into the transmitted sequence, as an insult of the noise.

Mutual information : $H(X:Y)=H(X)-H(X\mid Y)$ measures how much information $X$ and $Y$ have in common.

If the map from $X$ to $Y$ is one-to-one, then $H(X:Y)=H(X)$ telling us that all input information is shared. If the map from $X$ to $Y$ is totally random, that is, $X$ and $Y$ occurs independently, then $H(X:Y)=0$ since $H(X\mid Y)=H(X)$.

Shannon’s noisy coding theorem : $2^{NH(X:Y)}$ tells us the number of messages that can be reliably transmitted through the noisy channel.

Example : Binary symmetric channel : $X=\{0,1\},Y=\{0,1\}$.

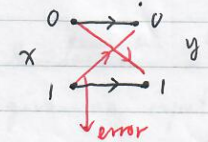
$$P(y=0\mid x=0)=1-f,P(y=0\mid x=1)=f,\\ P(y=1\mid x=0)=f,P(y=1\mid x=1)=1-f$$
where $f$ denotes the probability that a number is flipped. Let $f=0.15$ and $P(x=0)=0.9$ and $P(x=1)=0.1$. Determine $H(X),H(Y),H(Y\mid X)$ and $H(X:Y)$.

Solution :

$$H(X)=-0.9\times \log_20.9-0.1\log_20.1=0.47.$$

$$P(y=0)=P(y=0\mid x=0)P(x=0)+P(y=0\mid x=1)P(x=1)=0.78,\\ P(y=1)=0.22,H(Y)=0.76.\\ $$

$$\begin{align} H(Y\mid X)=&-\sum_i P(x_i)\sum_jP(y_j\mid x_i)\log P(y_j\mid x_i)\\ =&-0.9\times(0.85\times\log_20.85+0.15\times\log 0.15)\\ &+0.1\times(0.85\times\log_20.85+0.15\times\log 0.15)\\ =&0.61. \end{align}$$

$$H(X:Y)=H(Y)-H(Y\mid X)=0.15.$$

Suppose the length of a message is $N$. Using this source, we can only send $2^{0.15N}$ typical distinct messages instead of $2^{0.47N}$ under a noiseless channel.

$$H(X\mid Y)=H(X)-H(X:Y)=0.32.$$
Comparison between Boltzmann entropy and Shannon entropy

Boltzmann	Shannon
$S_B=-k_BN\sum_i p_i\log p_i$	$H=-\sum_i p_i\log p_i$
$p_i=e^{-\beta E_i}$, the probability that a particle occupies an energy level. $p_i$ is determined by energy.	$p_i$ is the probability that a letter $x_i$ occurs. $p_i$ is determined by a source.
$e^{S_B/k_B}$ measures the total number of configuration under such probability distribution.	$2^{NH}$ measures the total number of distinct typical messages with length being $N$.

Evidently, we can regard Boltzmann entropy as a special case of the Shannon entropy.

Capacity of a channel Q

$$C(Q)=\max_{P_X}\{H(X:Y)\}$$

the maximum mutual entropy in the distribution $P_X$. The distribution $P_X$ that achieves the maximum is called the optimal input distribution.

Example : Consider the binary symmetric channel with $f=0.15$. Above, we consider $P_X=\{P_0=0.9,P_1=0.1\}$ and found $I(X:Y)=0.15$ bits.

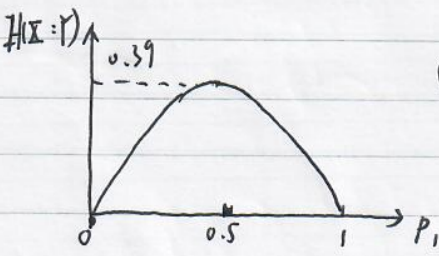
$C(Q_{BSC})=0.39$.

 The Physics of Information 信息物理