离散数学笔记（14）——欧拉图、哈密尔顿图与二部图

wzf2000
2019年12月18日

离散数学笔记（14）——欧拉图、哈密尔顿图与二部图

欧拉图、哈密尔顿图与二部图

欧拉图

欧拉迹

在无孤立结点的图 $G$ 中，如果存在一条路，它经过图中每条边一次且仅一次，称此路为欧拉迹。

欧拉回路

在无孤立结点的图 $G$ 中，若存在一条回路，它经过图中每条边一次且仅一次，称此回路为欧拉回路。

称此图为欧拉图，或 E 图（Euler）。

欧拉图判定

定理 1：一个非空连通图（可以是多重图）是欧拉图当且仅当它不含奇数度的点。

证明：前推后显然，后推前考虑反证法。

假设一个边数最少的图，使得其不存在欧拉回路。

取出连通图中最大的闭迹 $C$，则剩余边构成的子图中任意一个边数大于 $0$ 的分支 $G’$ 都满足不含奇数度的点的性质，故都具有一条欧拉回路 $C’$。

而因为 $G$ 的连通性，$\exists v \in V(C) \cap V(C’)$。（若不然，两个子图之间必定可以扩充）

则通过 $v$ 作为起点终点即可将 $C$ 与 $C’$ 合并得到 $CC’$ 获得一条 $G$ 的新的闭迹，与假设矛盾。

推论：一个连通图 $G$ 有欧拉迹当且仅当 $G$ 最多有两个奇点。

证明：前推后显然，后推前考虑将两个奇点之间连一条边，即可获得一条欧拉回路，再去掉这条边即得欧拉迹。

注：欧拉路与欧拉回路问题，也称一笔画问题。

定理 2：一个有向图 $D$ 具有欧拉迹，当且仅当 $D$ 是连通的，且除了两个顶点外，其余顶点的入度均等于出度。这两个特殊的顶点中一个顶点的入度比出度大 $1$，另一个顶点的入度比出度小 $1$。

求欧拉回路算法

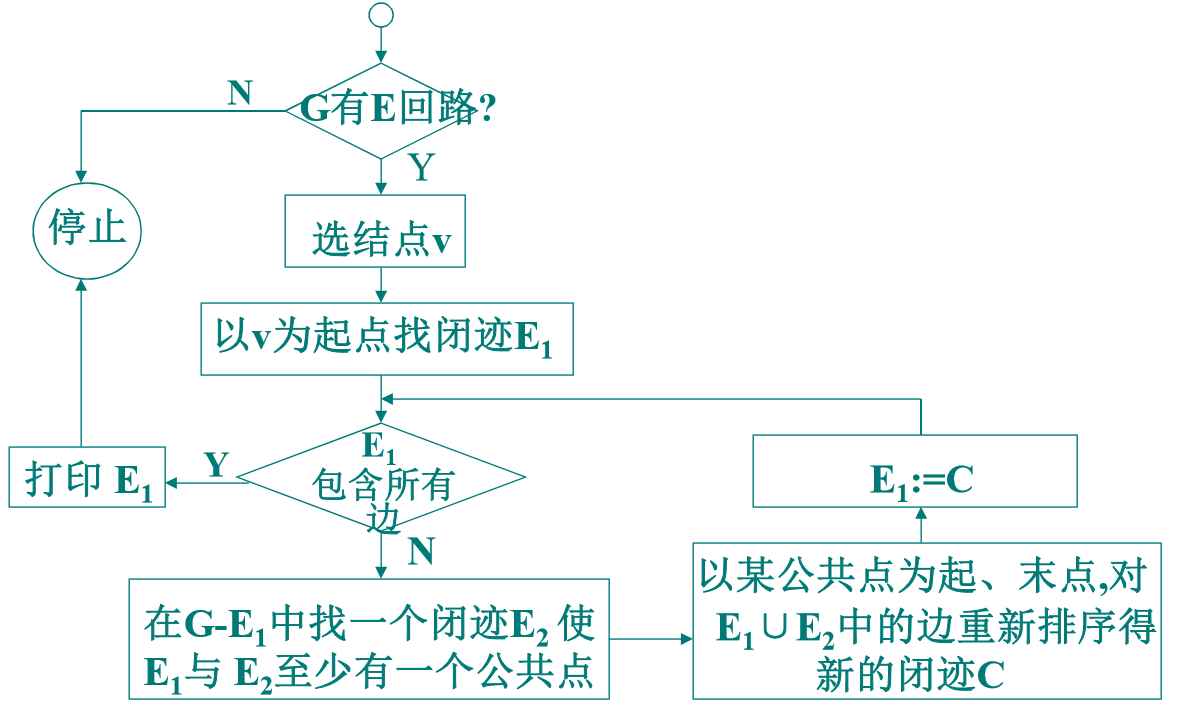
中国邮递员问题

一个邮递员送信，每次要走遍他负责投递范围内的街道，然后再回到邮局。问他应该按怎样的路线走，使所走的路程最短？

如果用点表示交叉路口，用点之间的连线表示对应的街道，每条线上对应一个实数，它是相应街道的长度。原问题变成一个图论问题。

中国邮递员问题：在赋以非负权的连通图 $G$ 上，求一条最小权环游。

环游：经过一个图 $G$ 的每条边至少一次的闭回路。

求解：

若 $G$ 中每个点的度为偶数，$G$ 为欧拉图，则 $G$ 中的欧拉回路是最优环游。

若 $G$ 不是欧拉图，则 $G$ 的任何环游，包括 $G$ 的最优环游，通过某些边将超过一次。

则问题变为：给出一个连通图 $G$。

1. 求 $E_1 \subseteq E$ 满足条件：在 $G$ 中重复 $E_1$ 中每条边，使得到的图 $G^*$ 是欧拉图（称这样的 $E_1$ 为可行集）。并且使 $E_1$ 的权尽可能小（称这样的可行集 $E_1$ 为最优集）。
2. 求 $G^*$ 的欧拉回路.。

定理：$L$ 是无向连通图 $G$ 最佳邮路（最优环游）的充要条件是：

1. $G$ 的每条路最多重复一次。
2. 在 $G$ 的任意一个回路上，重复边长度之和不超过该回路长度的一半。

特例：若 $G$ 恰好含两个奇点，则只需要重复此二奇点之间的最短路即可。

哈密顿图

哈密顿问题

用一个十二面体代表地球，用它的二十个顶点分别代表世界上的二十个城市。要求沿十二面体的棱，走过每个城市一次且仅仅一次，最后回到出发点。

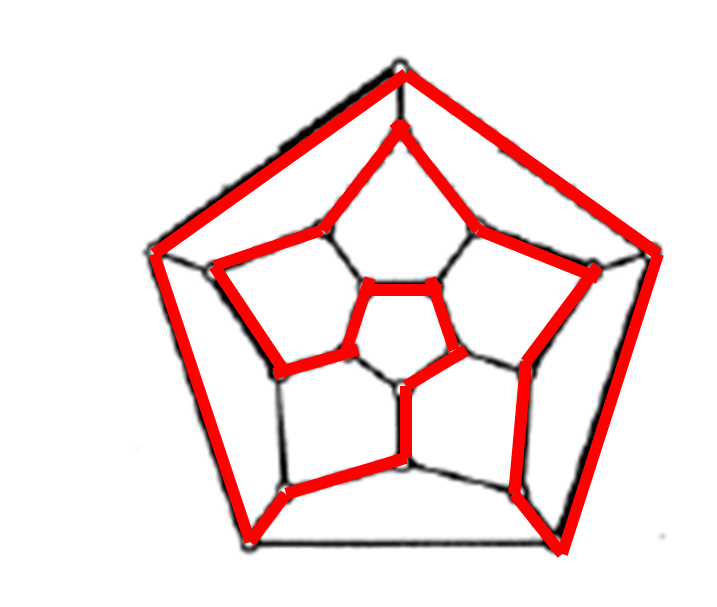
哈密顿图

设 $G = \langle V,E \rangle$ 是个无向有限图。

哈密顿路：通过 $G$ 中每个结点恰好一次的路。

哈密顿回路（H 圈）：通过 $G$ 中每个结点恰好一次的路。

哈密顿图（H 图）：具有哈密顿回路（H 全）的图。

设 $G$ 是多重图，$G’$ 是去掉 $G$ 中的多重边和环后得到的图，显然若 $G’$ 是 H 图，则 $G$ 也是 H 图，因此，只需讨论简单图。

哈密尔顿图的判定

定理 1（充分条件）：$G$ 是至少有 $3$ 个点的完全图，则 $G$ 是 $H$ 图。

定理 2：$G$ 是简单图，且 $n \ge 3$，若对 $G$ 中任一对不相邻点 $u,v$，都有 $d(u) + d(v) \ge n$ . 则 $G$ 是哈密顿图。

引理 1：设 $u,v$ 是 $G$ 的一对不相邻点，$d(u)+d(v) \ge n$。若 $G + uv$ 是 H 图 $\Leftrightarrow G$ 是 H 图。

定理 3：$G$ 是 H 图 $\Leftrightarrow C(G)$ 是 H 图。

定理 4：若 $C(G)=K_n \Leftrightarrow G$ 是 H 图。

定理 5：$G$ 是简单图，且 $n \ge 3, \delta \ge \frac{n}{2}$，则 $G$ 是 H 图。

定理 6：$G$ 是简单图，且 $n \ge 2$，若对 $G$ 中任一对不相邻点 $u,v$，都有 $d(u) + d(v) \ge n – 1$，则 $G$ 有 H 路。

利用此定理可得定理 2 另一种证明：

定理 7（必要条件）：若图 $G = \langle V,E \rangle$ 有 H 圈，则对 $V$ 的任何非空子集 $S$，均有 $W(G – S) \le |S|$，其中 $W(G – S)$ 是从 $G$ 中删去 $S$ 中所有结点及与这些结点关联的边所得到的子图的连通分支数。

定理 8：若 $G$ 是 Hamilton 圈 $\Rightarrow G$ 是 $2-$ 连通。

旅行商问题

H 圈问题不涉及边的长度，但是在许多实际问题中，每条边都可以有它的权。

旅行商问题（TSP）：一个商人欲到 $n$ 个城市推销商品，每两个城市 $i$ 和 $j$ 之间的距离为 $d_{ij}$，如何选择一条道路使得商人每个城市走一遍后回到起点，且所走路径最短。

图论语言：给定一个赋正权的完全图，求具有总长最短的 H 圈。

这个问题是 NPC 问题，一种好的精确求解法是分支与界法。

二部图

二部图

令 $G = \langle V,E \rangle$ 是无向图，如果可以将 $V$ 划分成两个子集 $V_1,V_2$，使得任何边 $(v_i,v_j) \in E$，$v_i \in V_1,v_j \in V_2$，则称 $G$ 是二部图，也称二分图，称 $V_1,V_2$ 是 $G$ 的互补的顶点子集。

完全二部图

令 $G = \langle V,E \rangle$ 是以 $V_1,V_2$ 为互补的顶点子集的二部图，如果 $V_1$ 中的每个节点都与 $V_2$ 中每个结点相邻接，则称 $G$ 是完全二部图。如果 $|V_1| = m,|V_2| = n$，则 $G$ 记作 $K_{m,n}$。

二部图的判定

定理：$G = \langle V,E \rangle$ 是二部图，当且仅当它的所有回路的长度都是偶数。

 离散数学 笔记