电子电路与系统基础笔记（5）——分压分流分析

电子电路与系统基础笔记（5）——分压分流分析

分压分流分析

电阻分压分流

电阻分压电路

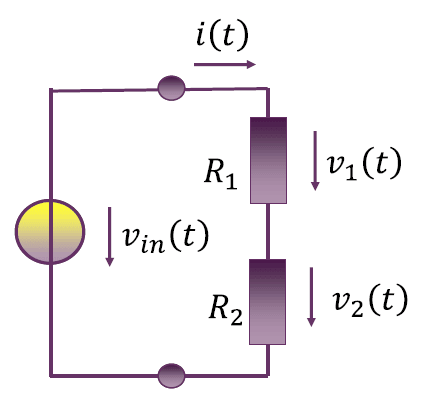
$$v_{in}(t) = v_1(t) + v_2(t) \\ v_1(t) = i(t) R_1 \\ v_2(t) = i(t) R_2 \\ v_{in}(t) = i(t)(R_1 + R_2) \\ i(t) = \frac{v_{in}(t)}{R_1 + R_2} \\ v_1(t) = \frac{R_1}{R_1 + R_2} v_{in}(t) \\ v_2(t) = \frac{R_2}{R_1 + R_2} v_{in}(t)$$
即得到分压系数。

等效电路

$$R_{in} = R_1 + R_2 \\ i(t) = \frac{v_{in}(t)}{R_{in}}$$

即可得到分压系数。

电阻分流电路

$$G_{in} = G_1 + G_2 \\ v_{in}(t) = \frac{i_{in}(t)}{G} \\ i_1(t) = \frac{G_1}{G_1 + G_2} i_{in}(t) = \frac{R_2}{R_1 + R_2} i_{in}(t) \\ i_2(t) = \frac{G_2}{G_1 + G_2} i_{in}(t) = \frac{R_1}{R_1 + R_2} i_{in}(t)$$
即可得到分流系数。

小结

• 串联总电阻等于串联分电阻之和，串联电阻上的分压系数为该电阻阻值比总电阻阻值。

$$v_m(t) = \gamma_{vm} v_{in}(t) = \frac{R_m}{R_{in}} v_{in}(t)$$

• 并联总电导等于并联分电导之和，并联电导上的分流系数为该电导导值比总电导导值。

$$i_m(t) = \gamma_{im} i_{in}(t) = \frac{G_m}{G_{in}} i_{in}(t)$$

电容分压分流

电容分压电路

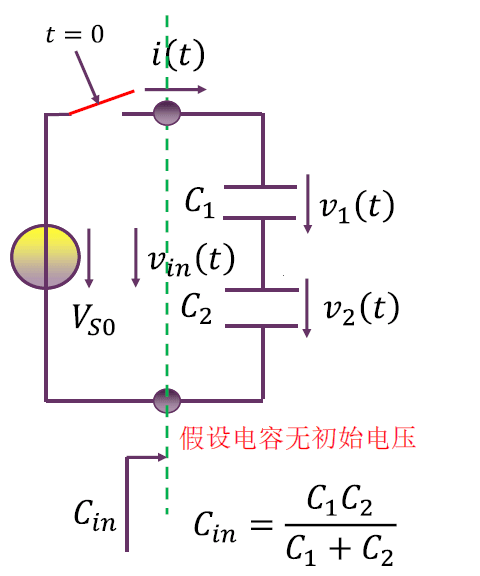
$$v_{in}(t) = V_{S0} U(t) \\ i(t) = C_{in} \frac{\mathrm{d}}{\mathrm{d} t} v_{in} (t) = C_{in} V_{S0} \delta (t) \\ v_1(t) = v_1(0^-) + \frac{1}{C_1} \int_{0^-}^t i(\tau) \mathrm{d} \tau \\ = \frac{C_{in} V_{S0}}{C_1} U(t) \\ = \frac{C_2}{C_1 + C_2} v_{in}(t) \\ v_2(t) = \frac{C_1}{C_1 + C_2} v_{in}(t)$$
即得出了分压系数。

实际上，容易发现，任意初始电压都是如此分压。

电容有初始电压

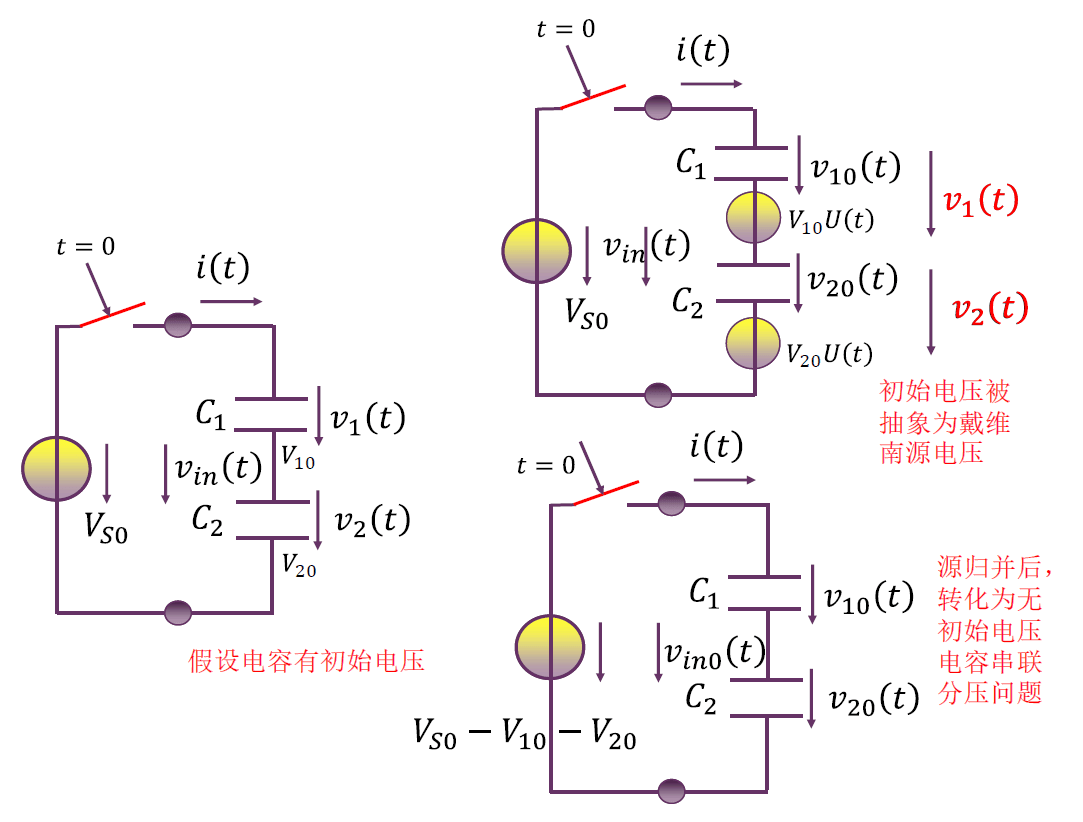
$$v_{in0}(t) = (V_{S0} – V_{10} – V_{20}) U(t) \\ v_{10}(t) = \frac{C_2}{C_1 + C_2} v_{in0}(t) \\ v_{20}(t) = \frac{C_1}{C_1 + C_2} v_{in0}(t) \\ v_1(t) = v_{10}(t) + V_{10} U(t) \\ v_2(t) = v_{20}(t) + V_{20} U(t)$$

叠加定理

• 表述 1：对于线性电路，如果电路中有多个源同时激励，则总响应为分响应之和。
  • 分响应：单独一个源起作用，其他源不起作用。
  • 源不起作用，就是将源置零，也就是恒压源短路处理，恒流源开路处理。
• 表述 2：对于线性电路，如果电路有多个源同时激励，则总响应可以表述为这些激励源的线性叠加形式。

小结

• 串联电容可以实现分压功能，分压系数为：

$$\gamma_{vCm} = \frac{\dfrac{1}{C_m}}{\sum\limits_{k = 1}^n \dfrac{1}{C_k}}$$

• 对偶地，并联电感可以实现分流功能，分流系数为：

$$\gamma_{iLm} = \frac{\dfrac{1}{L_m}}{\sum\limits_{k = 1}^n \dfrac{1}{L_k}}$$

有初值电容电感分压分流：把初值等效为源，用叠加定理处理。

电容分流电路

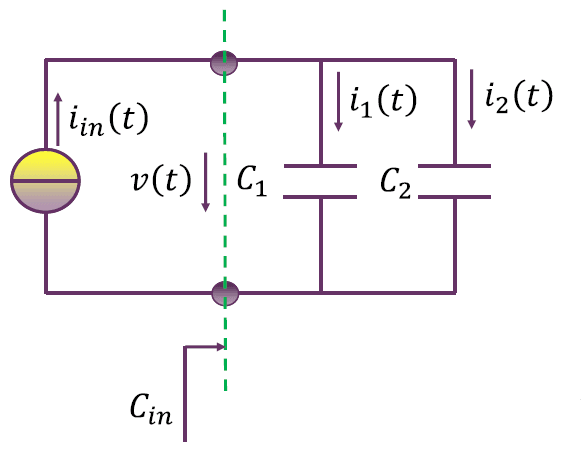
$$C_{in} = C_1 + C_2 \\ v(t) = \frac{1}{C_{in}} \int_{-\infty}^t i_{in}(\tau) \mathrm{d} \tau \\ i_1(t) = C_1 \frac{\mathrm{d}}{\mathrm{d} t} v(t) = \frac{C_1}{C_1 + C_2} i_{in}(t) \\ i_2(t) = C_2 \frac{\mathrm{d}}{\mathrm{d} t} v(t) = \frac{C_2}{C_1 + C_2} i_{in}(t)$$
即可得到分流系数。

利用对偶电路便可得出电感分压电路的分压系数。

小结

• 并联电容可以实现分流功能，分流系数为：

$$\gamma_{iCm} = \frac{C_m}{\sum\limits_{k = 1}^n C_k}$$

• 对偶地，串联电感可以实现分压功能，分压系数为：

$$\gamma_{vLm} = \frac{L_m}{\sum\limits_{k = 1}^n L_k}$$

阻容分压电路

纯阻、纯容、纯感串并联电路的分压分流关系（分压系数、分流系数）和激励信号形态无关，但RC、RL、RLC混合器件串并联电路的分压分流关系和激励信号形态（和时间）有关。

RC 串联电路：直流电压源激励

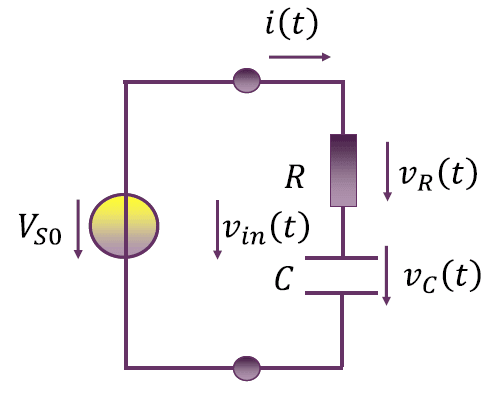
由于 RC 是线性时不变元件，不会产生新的频率分量，因此当直流激励时，电路中就只有一个直流（零频）分量。
直流信号可理解为是在 $t = -\infty$ 时加载的，经过无穷长时间后，电容初始电压（另一个源，叠加定理）的作用已经消失（指数衰减为 $0$ 了），因而直流分析不考虑初值问题。

$$v_{in}(t) = V_{S0} \\ v_R(t) = V_{R0} \\ v_c(t) = V_{C0}$$
直流激励只能是直流响应！
$$i(t) = i_C(t) = C \frac{\mathrm{d}}{\mathrm{d} t} v_C(t) = 0$$
直流情况下，电容相当于开路！
$$v_R(t) = i_R(t) R = i(t) R = 0 \\ v_C(t) = v_{in}(t) – v_R(t) = V_{S0}$$
电阻分压为 $0$，电容（直流开路）获得了全部的直流分压。

RC 串联电路：阶跃电压源激励

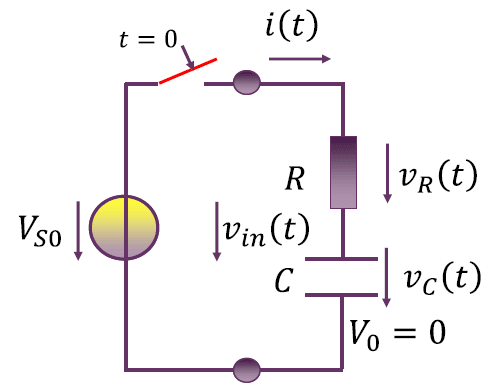
由于是线性电路，根据叠加定理，电阻分压和电容分压由两个源共同决定，第一个源为外加激励源 $v_S(t) = V_{S0}$，第二个源为电容初始电压 $V_0$ 的等效源，为了简单起见，首先假设 $V_0 = 0$，只考虑外加激励源单独作用的分压关系。

$$v_{in}(t) = V_{S0} U(t) \\ v_{in}(t) = Ri(t) + \frac{1}{C} \int_{-\infty}^t i(\lambda) \mathrm{d} \lambda \ \ \ (t \ge 0) \\ i(t) + \frac{1}{RC} \int_{-\infty}^t i(\lambda) \mathrm{d} \lambda = \frac{V_{S0}}{R} U(t) \\ \frac{\mathrm{d}}{\mathrm{d} t} i(t) + \frac{1}{RC} i(t) = \frac{V_{S0}}{R} \delta (t) \\ \frac{\mathrm{d}}{\mathrm{d} t} i(t) + \frac{1}{\tau} i(t) = \frac{V_{S0}}{R} \delta (t) \\ \tau = RC$$
称 $\tau$ 为时间常数。

求解微分方程可得：

$$\frac{\mathrm{d}}{\mathrm{d} t} \left ( e^{\frac{t}{\tau}} i(t) \right ) = \frac{V_{S0}}{R} e^{\frac{t}{\tau}} \delta (t) \\ e^{\frac{t}{\tau}} i(t) = \int_{-\infty}^t \frac{V_{S0}}{R} e^{\frac{\lambda}{\tau}} \delta (t) \mathrm{d} \lambda = \frac{V_{S0}}{R} U(t) \\ i(t) = \frac{V_{S0}}{R} e^{-\frac{t}{\tau}} U(t)$$
RC 电路的特征函数：指数衰减函数。

其中冲激函数的取样特性：

$$\int_{-\infty}^{+\infty} f(t) \delta(t) \mathrm{d} t \\ = f(0) \int_{-\infty}^{+\infty} \delta(t) \mathrm{d} t = f(0)$$

零状态响应

$V_0 = 0$，电容初始状态为 $0$ 的分析，称此时的响应为零状态响应。

$$v_R(t) = i(t)R = V_{S0} e^{-\frac{t}{\tau}} U(t) \\ v_C(t) = v_{in}(t) – v_R(t) \\ = V_{S0} \left( 1 – e^{-\frac{t}{\tau}} \right ) U(t)$$
可知 RC 分压是时间的函数，故称之为动态电路。

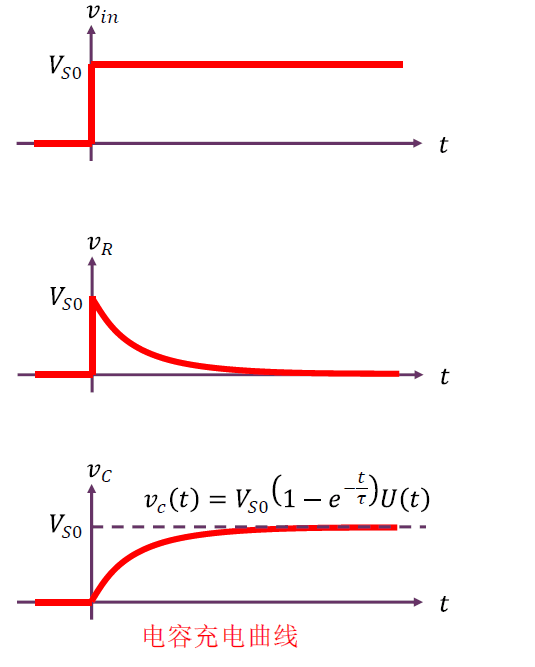
电容的信号特性

直流开路，高频短路。

$$i_C(t) = C \frac{\mathrm{d}}{\mathrm{d} t} v_C(t) = C \frac{\mathrm{d}}{\mathrm{d} t} V_0 = 0 \\ v_C(t) = \frac{1}{C} \int_{-\infty}^t i(\tau) \mathrm{d} \tau = \frac{1}{C} \int_{-\infty}^t I_0 \cos \omega \tau \mathrm{d} \tau = \frac{I_0}{\omega C} \sin \omega t \to 0 (\omega \to \infty)$$

信号的微分值和频率成正比，微分值很大代表高频，微分值很小代表低频。

阶跃响应看通带

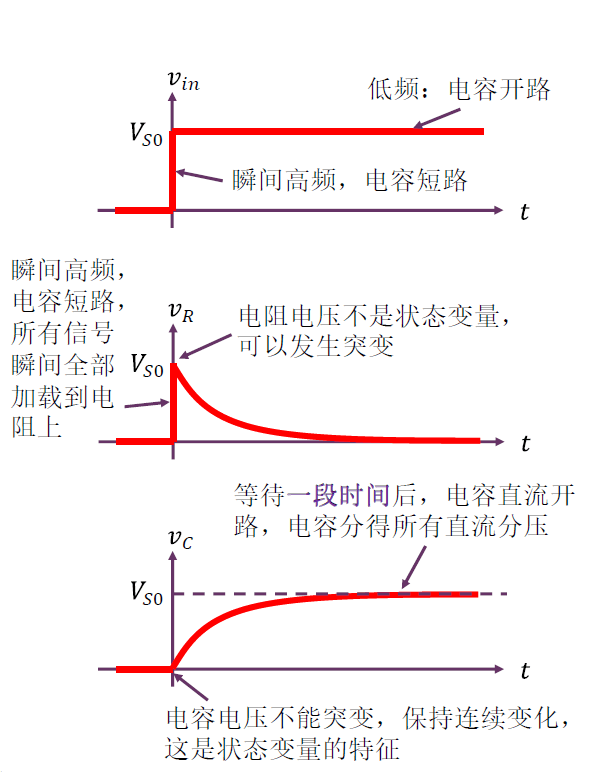
电容充电曲线

工程上认为 $5\tau$ 时间后，电容充电结束，进入稳态。

电容电压不能突变，电容电压瞬间为 $0$，电容瞬间阻抗为零（电容高频短路），回路初始电流为 $\frac{V_{S0}}{R}$，该电流对电容充电，短时内电容电压线性上升，导致回路电流降低，充电电流减小，充电速率（斜率）下降，最终呈现出指数衰减规律：当电容电压等于输入电压时，回路电流为零，不再对电容充电，电容电压稳定在输入电压上：$5 \tau$ 时间后，阶跃信号可理解为看不到跳变了，只看到直流，电容直流开路，全部直流电压加载到电容上。

零输入响应

等效电路分析

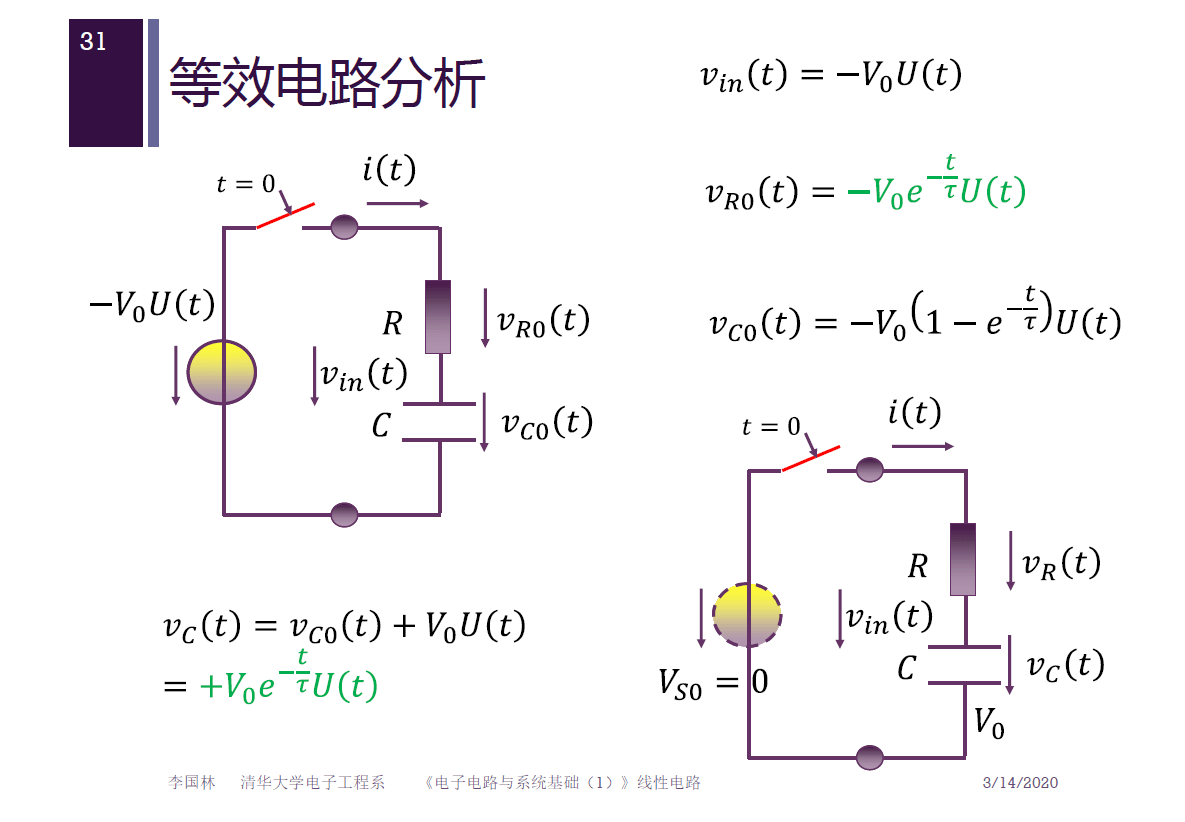
可以发现电容放电。

工程上一般认为 $5 \tau$ 后，电容电压趋于稳态值。

开关闭合瞬间，电容电压全部加载到电阻上，形成放电电流 $\frac{V_0}{R}$，该电流对电容放电，短时内电容电压线性下降，导致加载到电阻上的电压随之下降，放电电流降低，放电速率（斜率）下降，最终呈现出指数衰减规律：当电容电压下降为零时，放电电流为零，电容不再放电。

全响应 $=$ 零状态响应 $+$ 零输入响应

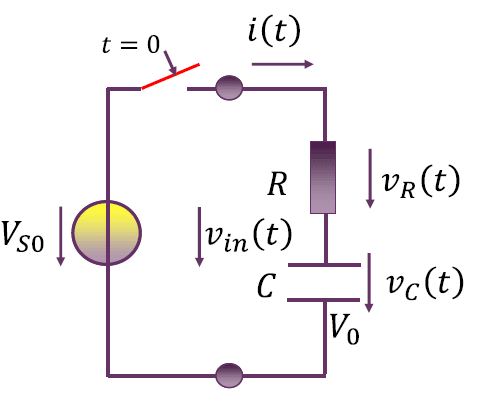
由于是线性电路，根据叠加定理，总响应等于分响应之和，因此全响应等于零状态响应和零输入响应之和。

$$t \ge 0 : \\ v_R(t) = (V_{S0} – V_0) e^{-\frac{t}{\tau}} U(t) \\ v_C(t) = V_{S0} \left (1 – e^{-\frac{t}{\tau}} \right ) U(t) + V_0 e^{-\frac{t}{\tau}} U(t) \\ t < 0 : \\ v_R(t) = 0 \\ v_C(t) = V_0$$ 对应曲线为：

RL 并联电路：阶跃电流源激励

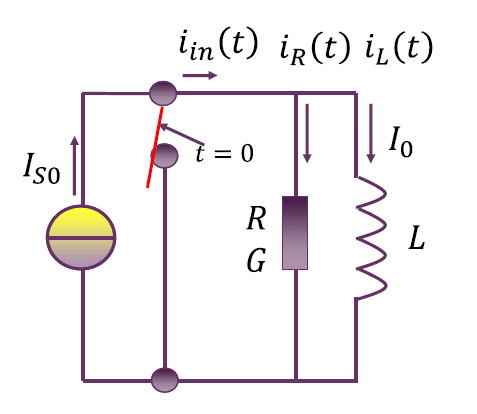
$$i_R(t) = (I_{S0} – I_0) e^{-\frac{t}{\tau}} U(t) \\ i_L(t) = (I_{S0} – I_0) \left ( 1 – e^{-\frac{t}{\tau}} \right ) U(t) + I_0 \\ \tau = GL$$

零响应状态：电感充磁

$$i_L(t) = \frac{1}{L} \int_{-\infty}^t v_L(t) \mathrm{d} t = \frac{1}{L} = \int_0^t v_L(t) \mathrm{d} t$$

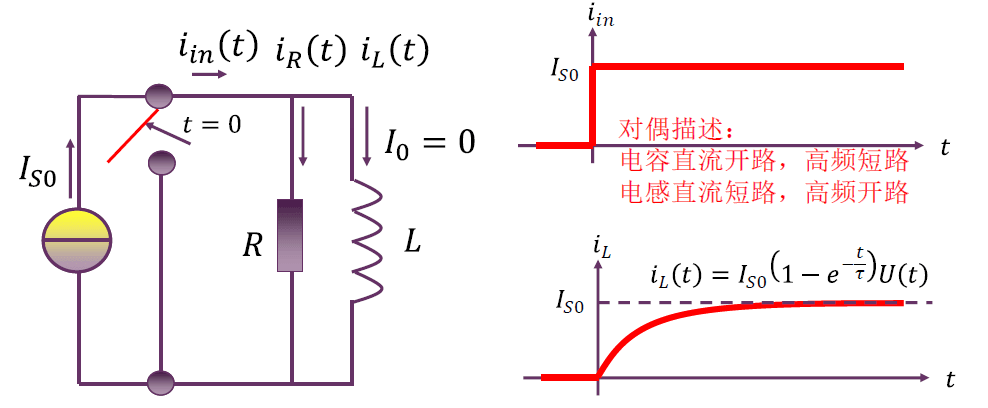
电感电流不能突变，电感电流瞬间为 $0$，电感瞬间阻抗为无穷（电感高频开路），结点初始电压为 $I_{S0} R$，该电压对电感充磁，短时内电感电流线性上升，导致电阻分流变小，结点电压下降，充磁电压下降，充磁速率（斜率）下降，最终呈现出指数衰减规律：当电感电流等于输入电流时，电阻分流为 $0$，电阻电压即结点电压为零，不再对电感充磁，电感电流稳定在输入电流上：$5 \tau$ 时间后，阶跃信号可理解为看不到跳变了，只看到直流，电感直流短路，全部直流电电流加载到电感上。

零输入相应：电感放磁

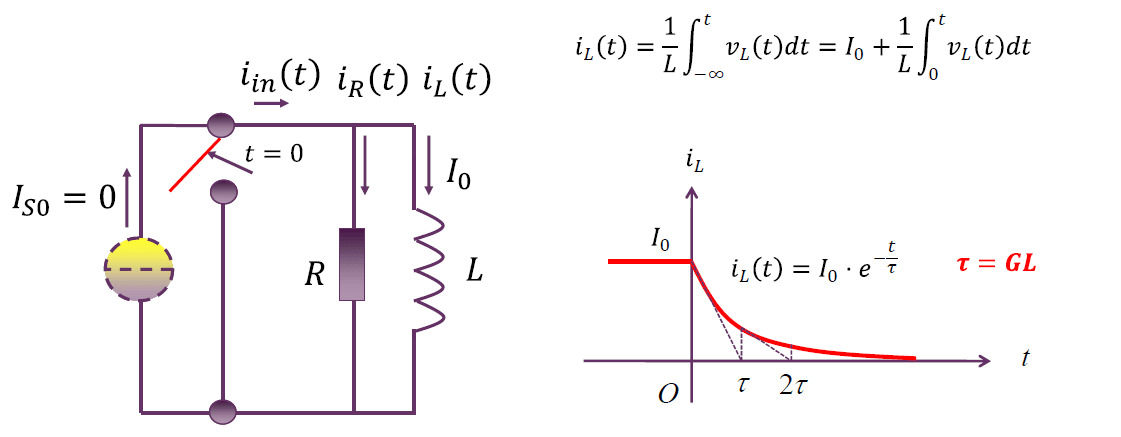
开关断开瞬间，电感电流全部加载到电阻上，形成放磁电压 $-I_0 R$，该电压对电感放磁，短时内电感电流线性下降，导致加载到电阻上的电流随之下降，放磁电压降低，放磁速率（斜率）下降，最终呈现出指数衰减规律：当电感电流下降为零时，放磁电压为零，电感不再放磁。

小结

• 电容具有直流开路，高频短路的信号特性；对偶地，电感具有直流短路，高频开路的信号特性。
• 对于一阶 RC 电路或一阶 RL 电路，描述电路的特征参量为时间常数 $\tau$。
  • $\tau = RC;\tau = GL$
• RC 分压电路：直流激励时，电容开路，获得所有直流分压，电阻分压为 $0$；阶跃信号 $V_{S0} U(t)$ 激励时，电容瞬间短路（$t = 0$），所有电压 $V_{S0}$ 全部加载电阻上，等待足够长时间（$t > 5 \tau$）后，电容直流开路，所有电压 $V_{S0}$ 全部加载电容上，因此电容电压存在一个由 $0$ 变化到 $V_{S0}$、电阻电压存在一个由 $V_{S0}$ 变化到 $0$ 的变化过程，这个变化过程是指数衰减过程，指数衰减时间常数为 $\tau$。
• 当电容或电感有初值时，这些初值就是电路内蕴的源。由于 RC、RL 电路为线性电路，根据叠加定理，电路总响应为零状态响应和零输入响应之和。
  • 对于一阶 RC 电路，零状态响应为电容充电过程，零输入响应为电容放电过程。

 电电 笔记