复变函数引论笔记（3）——复变函数的积分

复变函数引论笔记（3）——复变函数的积分

Chapter 3. 复变函数的积分

1. 积分的概念

1.1. 定义

$w = f(z)$ 在 $D$ 上有定义，有向曲线 $C \subseteq D$ 规定了方向，$C^-$ 表示反方向。（先约定 $C$ 是光滑曲线）

将 $C$ 分成 $n$ 个弧段，分点为 $z_0 = A, z_1, \cdots, z_{n – 1}, z_n = B$，且每个弧段 $\overset{\Huge{\frown}}{z_{i – 1} z_i}$ 上取点 $\zeta_k = \xi_k + \mathrm{i} \eta_k \ (k = 1, \cdots, n)$。

和式：

$$I_0 = \sum_{k = 1}^n f(\zeta_k) \Delta z_k \quad (\Delta z_k = z_k – z_{k – 1})$$
记 $\Delta s_k = \overset{\Huge{\frown}}{z_{i – 1} z_i}$ 的长度，$n \to \infty$ 且 $\delta \to 0$ 时，若不论分法以及 $\zeta_k$ 取值如何，$I_n$ 均有唯一极限 $I \in \mathbb{C}$，则称 $f(z)$ 沿 $C$ 是可积分。

$I$ 称为 $f(z)$ 沿 $C$ 的积分，记作：

$$I = \int_C f(z) \, dz = \lim_{n \to \infty} \sum_{k = 1}^n f(\zeta_k) \Delta z_k$$
若 $C$ 是封闭曲线，积分记为：
$$I = \oint_C f(z) \, d z$$

1.2. 积分存在的条件及其计算法

先假设 $f(z)$ 沿着分段光滑曲线 $C$ 是连续的：

$$\begin{align*} I_n & = \sum_{k = 1}^n (u(\xi_k, \eta_k) + \mathrm{i} v(\xi_k, \eta_k)) (\Delta x_k + \Delta y_k) \\ & = \sum_{i = 1}^n \left\{\left[u(\xi_k, \eta_k) \Delta x_k – v(\xi_k, \eta_k) \Delta y_k\right] + \mathrm{i} \left[v(\xi_k, \eta_k) \Delta x_k + u(\xi_k, \eta_k) \Delta y_k\right]\right\} \\ \end{align*}$$
可知：
$$\begin{align*} & \quad \int_C u \, dx – v \, dy + \mathrm{i} \int_C v \, dx + u \, dy \\ & = I = \int_C f(z) \, dz \end{align*}$$
当 $C: z = z(t) = x(t) + \mathrm{i} y(t), t \in [a, b]$ 时：
$$\int_C f(z) \, dz = \int_a^b \{u[x(t), y(t)] + \mathrm{i} v[x(t), y(t)]\} \{x^\prime(t) + \mathrm{i} y^\prime(t)\} \, dt = \int_a^b f[z(t)] z^\prime(t) \, dt$$

1.3. 积分性质

性质：

1. $\displaystyle \int_{C^-} f(z) \, dz = – \int_C f(z) \, dz$
2. $\displaystyle \int_C k f(z) \, dz = k \int_C f(z) \, dz, k = const$
3. $\displaystyle \int_C (f(z) \pm g(z)) \, dz = \int_C f(z) \, dz \pm \int_C g(z) \, dz$

4. 设 $w = f(z)$ 在 $C$ 上满足 $|f(z)| \le M, \forall z \in C$，则：

   $$\left|\int_C f(z) \, dz \right| \le \int_C |f(z)| \, |dz| \le \int_C M |dz| = \int_C M ds = ML$$

   其中 $L$ 为 $C$ 弧长。

对于分段光滑曲线 $C = C_1 + \cdots +C_m$：

$$\int_C f(z) \, dz \stackrel{\triangle}{=} \sum_{k = 1}^m \int_{C_k} f(z) \, dz$$

2. Cauchy-Goursat 基本定理

2.1. 回忆 Green 公式

Green 公式：

设 $D$ 是 Jordan 区域，$P(x, y), Q(x, y) \in C^1(D), C \subseteq D$ 是一条 Jordan 闭曲线，其围成的 Jordan 区域为 $B$，则：

$$\oint_C P \, dx + Q \, dy = \iint_B \left(\frac{\partial Q}{\partial x} – \frac{\partial P}{\partial y} \right) \, dx \, dy$$
假设 $w = f(z) = u + \mathrm{i} v$ 在 $D$ 上解析，假设 $u, v \in C^1(D)$，可发现：
$$\begin{align*} \oint_C f(z) \, dz & = \int_C u \, dx – v \, dy + \mathrm{i} \int_C v \, dx + u \, dy \\ & = \iint_B \left(-\frac{\partial v}{\partial x} – \frac{\partial u}{\partial y} \right) \, dx \, dy + \mathrm{i} \iint_B \left(\frac{\partial u}{\partial x} – \frac{\partial v}{\partial y} \right) \, dx \, dy \\ & = 0 \end{align*}$$
但实际上，$u, v \in C^1(D)$ 实际上为后置性质，也就是可以通过上述推出的条件推出。

2.2. Cauchy-Goursat 定理

Cauchy-Gourset 定理：

设 $w = f(z)$ 在 Jordan 区域 $D$ 上解析，$C \subseteq D$ 是 $D$ 内任意一条封闭曲线，则：

$$\oint_C f(z) \, dz = 0$$
（证明可考虑区间套定理）

2.3. 加强的 Cauchy-Goursat 定理

设 $w = f(z)$ 在由 Jordan 闭曲线 $\gamma$ 围成的 Jordan 区域 $D$ 上解析，在 $\overline{D} = D \cup \gamma$ 上是连续的，则：

$$\oint_\gamma f(z) \, dz = 0$$
注：如果区域内单点不满足，定理会变成如何？（留数定理）

3. 复合闭路定理

3.1. 闭路变形原理

定理：

一个解析函数沿闭曲线的积分，不会因为曲线的连续变形而改变。

即：

$$\int_{C_2 + C_1^-} f(z) \, dz = 0$$
可以通过简单的闭合曲线拼接得到。

3.2. 复合闭路定理

定义：

如图所示，由 $\gamma = \gamma_0 + \gamma_1^- + \cdots + \gamma_n^-$ 构成复合闭路。

其中 $\gamma_0$ 为最外层的闭合曲线，其他分别是内部的闭合曲线。

定理：

设 $\omega = f(z)$ 在由上述复合闭路围成的区域 $D$ 上是解析的，在 $\overline{D} = D \cup \gamma$ 上是连续的，则：

$$\oint_\gamma f(z) \, dz = 0$$
证明类似上面的想法。

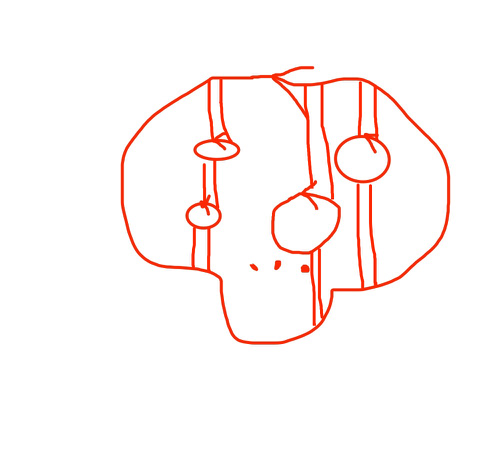
$e.g.$

$$\oint_{|z – z_0| = r} \frac{dz}{(z – z_0)^{n + 1}} = \begin{cases} 2 \pi \mathrm{i} & n = 0 \\ 0 & n \not = 0 \end{cases}$$

4. 原函数与不定积分

4.1. 定义

下设 $w = f(z)$ 在单连通区域 $D$ 上是解析的。

定义：

固定 $z_0$ 有：

$$F(z) = \int_{z_0}^z f(\zeta) \, d \zeta$$
（well defined）

定理 1：

$f(z)$ 如前假设，则 $F(z)$ 在 $D$ 上是解析的，且 $F^\prime(z) = f(z), \forall z \in D$。

证明：

$$\begin{align*} F(z + \Delta z) – F(z) & = \int_{z_0}^{z + \Delta z} f(\zeta) \, d \zeta – \int_{z_0}^z f(\zeta) d \zeta \\ & = \int_z^{z + \Delta z} f(\zeta) \, d \zeta \\ & = \int_z^{z + \Delta z} [f(z) + f(\zeta) – f(z)] \, d \zeta \\ & = f(z) \Delta z + \int_z^{z + \Delta z} [f(\zeta) – f(z)] \, d \zeta \\ & = f(z) \Delta z + \Delta z \int_z^{z + \Delta z} \frac{f(\zeta) – f(z)}{\Delta z} \, d \zeta \end{align*}$$
只须证明：
$$\int_z^{z + \Delta z} \frac{f(\zeta) – f(z)}{\Delta z} \, d \zeta$$
是无穷小量。

任意 $\varepsilon > 0$，当 $|\zeta – z| << 1$ 时（足够小时），总能使得 $|f(z) - f(\zeta)| < \varepsilon$，因此：

$$\left|\int_z^{z + \Delta z} \frac{f(\zeta) - f(z)}{\Delta z} \, d \zeta\right| \le \frac{1}{|\Delta z|} \int_z^{z + \Delta z} |f(\zeta) - f(z)| \, d \zeta \le \frac{1}{|\Delta z|} \cdot \varepsilon \cdot |\Delta z| = \varepsilon$$ 定义：

设在区域 $D$ 上函数 $F(z)$ 满足 $F^\prime(z) = f(z), \forall z \in D$，则称 $F(z)$ 是 $f(z)$ 在 $D$ 上的一个原函数。

任意 $f(z)$ 两个原函数之间只相差一个常数。

$F(z) + c$ 称为 $f(z)$ 的不定积分，记作：

$$F(z) + c = \int f(\zeta) \, d \zeta$$

4.2. 定理

定理 2（N-L 公式）：

设 $w = f(z)$ 在单连通区域 $D$ 上解析，$F(z)$ 为 $f(z)$ 在 $D$ 上一个原函数，$\forall z_0, z_1 \in D$，则：

$$\int_{z_0}^{z_1} f(z) \, dz = F(z) \Bigg |_{z_0}^{z_1}$$
定理 3：

设 $f(z), g(z)$ 在单连通区域 $D$ 上解析，$z_0, z_1 \in D$，则：

$$\int_{z_0}^{z_1} f(z) g^\prime(z) \, dz = f(z) g(z) \Bigg |_{z_0}^{z_1} – \int_{z_0}^{z_1} f^\prime(z) g(z) \, dz$$
定理 4：

设 $w = f(z)$ 在 $D$ 上解析，则下面三条是等价的：

1. $f(z)$ 沿 $D$ 中任意一个回路积分为 $0$。
2. $f(z)$ 在 $D$ 中具有积分路径无关性。
3. $f(z)$ 在 $D$ 上有原函数。

其中 3 推 2：

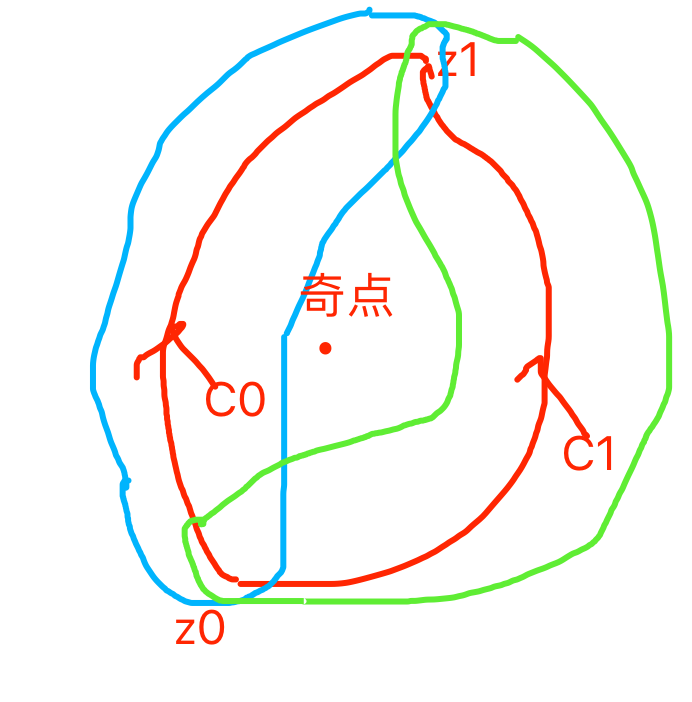
$F^\prime(z) = f(z), z \in D$，假设从 $z_0$ 到 $z_1$ 有两条无法连续变形的曲线 $C_1, C_2$（包含了奇点）。

而 $C_1, C_2$ 分别可以看作在两个不同的单连通区域上（蓝色和绿色区域），根据 N-L 公式，即可得沿 $C_1$ 和 $C_2$ 的积分都是：

$$F(z) \Bigg |_{z_0}^{z_1}$$

5. Cauchy 积分公式

5.1. Cauchy 积分公式

定理：

设 $w = f(z)$ 在由 Jordan 闭曲线 $\gamma$ 围成的单连通区域 $D$ 上解析，在 $\overline{D} = D \cup \gamma$ 上连续，则对 $\forall z_0 \in D$ 有 Cauchy 积分公式：

$$f(z_0) = \frac{1}{2\pi \mathrm{i}} \oint_\gamma \frac{f(z) \, dz}{z – z_0}$$

证明：

右边可以化为：

$$\frac{1}{2 \pi \mathrm{i}} \oint_{C_r} \frac{f(z) \, dz}{z – z_0} = \frac{1}{2 \pi \mathrm{i}} \oint_{C_r} \frac{f(z_0) + (f(z) – f(z_0))}{z – z_0} \, dz = f(z_0) + E$$
其中：
$$E = \frac{1}{2 \pi \mathrm{i}} \oint_{C_r} \frac{f(z) – f(z_0)}{z – z_0} \, dz$$
而考虑：
$$|E| \le \frac{1}{2 \pi} \oint_{C_r} \frac{|f(z) – f(z_0)| \, |dz|}{|z – z_0|} = \frac{1}{2 \pi r} \oint_{C_r} |f(z) – f(z_0)| \, ds \le \frac{1}{2 \pi r} \oint_{C_r} \varepsilon \, ds = \varepsilon$$
当 $r << 1$ 时，$|f(z) - f(z_0)| < \varepsilon$，因此 $E$ 是无穷小量，故 $E = 0$，公式即得证。$\square$

6. 解析函数的高阶导数

6.1. 解析函数的导数也解析

定理：

设 $w = f(z)$ 在 $D$ 上解析，则对 $\forall z_0 \in D$ 有：

$$f^{(n)}(z_0) = \frac{n!}{2 \pi \mathrm{i}} \oint_{C} \frac{f(z) \, dz}{(z – z_0)^{n + 1}} \quad (n \ge 1)$$
其中 $C \subseteq D$ 是一条环绕 $z_0$ 的 Jordan 闭曲线，其内部区域完全含于 $D$。

证明：

只证明 $n = 1$ 时成立。

$i.e.$

$$f^\prime(z_0) = \frac{1}{2 \pi \mathrm{i}} \oint_C \frac{f(z) \, dz}{(z – z_0)^2}$$
考虑 $C$ 为以 $z_0$ 为圆心半径 $r$ 的圆周，令 $|\Delta z| < \dfrac{r}{2}$： $$\frac{f(z_0 + \Delta z) - f(z_0)}{\Delta z} = \frac{1}{2 \pi \mathrm{i} \Delta z} \left[\oint_{C} \frac{f(z) \, dz}{z - \Delta z - z_0} - \oint_{C} \frac{f(z) \, dz}{z - z_0} \right] = \frac{1}{2 \pi \mathrm{i}} \oint_C \frac{f(z) \, dz}{(z - z_0)(z - z_0 - \Delta z)} \\ = \frac{1}{2 \pi \mathrm{i}} \oint_C \frac{[z - (z_0 + \Delta z) + \Delta z] f(z) \, dz}{(z - z_0)^2 [z - (z_0 + \Delta z)]} = \frac{1}{2 \pi \mathrm{i}} \oint_C \frac{f(z) \, dz}{(z - z_0)^2} + E$$ 其中： $$E = \frac{1}{2 \pi \mathrm{i}} \oint_C \frac{\Delta z f(z) \, dz}{[z - (z_0 + \Delta z)](z - z_0)^2}$$ 而： $$|E| \le \frac{\Delta z}{2 \pi} \oint_C \frac{|f(z)| \, |dz|}{|(z - z_0) - \Delta z||z - z_0|^2} \\ |(z - z_0) - \Delta z| \ge |z - z_0| - |\Delta z| = r - |\Delta z| > \frac{r}{2} \\ |E| \le \frac{|\Delta z|}{2 \pi} \oint_C \frac{M \, ds}{r^2 \dfrac{r}{2}} = \frac{2 M |\Delta z|}{r^2} \to 0 \quad (\Delta z \to 0)$$
其中：
$$M = \max_{|z – z_0| \le r} |f(z)|$$
故得证。$\square$

6.2. 解析的充要条件——Morera 定理

设 $w = f(z)$ 在单连通区域上满足：

$$\oint_C f(z) \, dz = 0, \forall C \subseteq D$$
则 $f(z)$ 在 $D$ 上解析？

可取：

$$f(z) = \begin{cases} 0 & z \not = 0 \\ 1 & z = 0 \end{cases}$$
是上述反例。

但是只须加上 $w = f(z)$ 在 $D$ 上连续，即可得到正确命题。

Morera 定理：

设 $w = f(z)$ 在连通区域上连续且：

$$\oint_C f(z) \, dz = 0, \forall C \subseteq D$$
则 $f(z)$ 在 $D$ 上解析。

证明：

设：

$$F(z) = \int_{z_0}^z f(\zeta) \, d \zeta$$
只须证明：
$$F^\prime(z) = f(z)$$
可类比第 $4$ 节的定理 1 证明得到，故可得 $F(z)$ 为解析函数，则 $f(z)$ 作为其导函数也解析。$\square$

6.3. Cauchy 不等式

设 $w = f(z)$ 在 $|z – z_0| < R$ 上解析且 $|f(z)| \le M(\forall z \in D)$，则对 $\forall m \ge 1$ 有：

$$|f^{(n)}(z_0)| \le \frac{n! M}{R^n}$$ 证明：
$$f^{(n)} (z_0) = \frac{n!}{2 \pi \mathrm{i}} \oint_{C_r} \frac{f(z) \, dz}{(z – z_0)^{n + 1}}, \forall 0 < r < R \\ \Rightarrow |f^{(n)}(z_0)| \le \frac{n!}{2 \pi} \oint_{C_r} \frac{|f(z)| \, |dz|}{|z - z_0|^{n + 1}} \\ \le \frac{n!}{2 \pi} \oint_{C_r} \frac{M \, ds}{r^{n + 1}} = \frac{n! M}{r^n} \\ \Rightarrow |f^{(n)}(z_0)| \le \frac{n! M}{R^n}$$ 最后一步两侧取极限即可。$\square$

6.4. Liouville 定理

设 $w = f(z)$ 是有界整函数，则：

$$f(z) \equiv const$$
证明：

$\forall z_0 \in \mathbb{C}, |f^\prime(z_0)| \le \dfrac{1! M}{R}$，令 $R \to +\infty$，可得 $f^\prime(z) \equiv 0 \Rightarrow f(z) \equiv const$。$\square$

6.5. 代数基本定理

$$P_n(z) = a_n z^n + \cdots + a_1 z + a_0, a_n \not = 0$$

代数基本定理：

$p_n(z) = 0$ 在 $\mathbb{C}$ 上恰好有 $n$ 个根（计算重数）。

证明：

只须证明 $p_n(z)$ 在 $\mathbb{C}$ 上至少有一个零点。（$P_n(z) = (z – z_1) P_{n – 1}(z)$）

考虑反证，假设：

$$P_n(z) \not = 0, \forall z \in \mathbb{C}$$
令：
$$f(z) = \frac{1}{P_n(z)}$$
则 $f(z)$ 为整函数。

由于 $P_n(z) \to \infty(z \to \infty)$，因此 $|P_n(z)| \to +\infty(z \to \infty)$。

因此将 $\mathbb{C}$ 分为有界、无界两部分，即可得到 $f(z)$ 有界。

根据 Liouville 定理，即得 $f(z) \equiv const$，可推出矛盾。$\square$

7. 解析函数与调和函数

7.1. 调和函数

定义：

设 $\varphi = \varphi(x, y) \in C^2(D)$，若在 $D$ 上处处有：

$$\Delta \varphi = \frac{\partial^2 \varphi}{\partial x^2} + \frac{\partial^2 \varphi}{\partial y^2} = 0$$
则称 $\varphi$ 是 $D$ 上调和函数。

$\Delta$——拉普拉斯算子。

7.2. 解析函数与调和函数

$f(z) = u(x, y) + \mathrm{i} v(x, y)$ 在 $D$ 上解析，$u, v \in C^\infty(D)$：

$$\Delta u = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = \frac{\partial}{\partial x} \left(\frac{\partial v}{\partial y} \right) + \frac{\partial}{\partial y} \left(- \frac{\partial v}{\partial x} \right) = 0 \\ \Delta v = 0$$
定理：

设 $w = f(z) = u + \mathrm{i} v$ 在 $D$ 上解析，则 $u, v$ 均在 $D$ 上调和。

定义：

如上假设，$v$ 称为 $u$ 在 $D$ 上的共轭调和函数。

问题：

$u = u(x, y)$ 在 $D$ 上调和，是否能找到它在 $D$ 上的共轭调和函数？（$u + \mathrm{i} v$ 在 $D$ 上解析）

定理：

设 $u = u(x, y)$ 是单连通区域 $D$ 上调和函数，则 $\exists v = v(x, y)$ 是 $D$ 上调和函数，$s.t. \ w = f(z) = u + \mathrm{i} v$ 在 $D$ 上解析。

证明：

可验证：

$$U(z) \stackrel{\triangle}{=} u_x – \mathrm{i} u_y$$
其在 $D$ 上解析。

则：

$$f(z) = \int U(z) \, dz = u + \mathrm{i} v$$
$u$ 确定，但 $v$ 可以差一常数。$\square$

 复变 笔记